题目内容
如图，在平面直角坐标系xOy中，两反比例函数y=| k1 |
| x |
| k2 |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：反比例函数图象上点的坐标特征
专题：
分析：直接根据反比例函数系数k的几何意义进行解答，用k1和k2表示矩形的面积，然后用QN和MP分别表示，利用等量代换法求出MP和QN的比．
解答：
解：∵点Q、N分别在反比例函数y1=
，y2=
的图象上，作QE⊥x轴，ND⊥x轴，
∴S矩形OEQC=k1，S矩形ODNC=k2
∴S矩形EDNQ=S矩形ODNC-S矩形OEQC=k2-k1=QN•OC=3QN．
又∵点P、M分别在反比例函数y1=
，y2=
的图象上，作MF⊥y轴，PG⊥y轴，
∴S矩形OAPG=k1，S矩形OAMF=k2
∴S矩形GPMF=SOAMF-S矩形OAPG=k2-k1=MP•OA=4MP．
∴3QN=4MP
∴
=
．
解：∵点Q、N分别在反比例函数y1=| k1 |
| x |
| k2 |
| x |
∴S矩形OEQC=k1，S矩形ODNC=k2
∴S矩形EDNQ=S矩形ODNC-S矩形OEQC=k2-k1=QN•OC=3QN．
又∵点P、M分别在反比例函数y1=
| k1 |
| x |
| k2 |
| x |
∴S矩形OAPG=k1，S矩形OAMF=k2
∴S矩形GPMF=SOAMF-S矩形OAPG=k2-k1=MP•OA=4MP．
∴3QN=4MP
∴
| MP |
| QN |
| 3 |
| 4 |
点评：考查反比例函数图象上坐标的特点和k的几何意义，结合图形分析出之间的数量关系．
练习册系列答案
相关题目
如果n=
成立，那么直角坐标系中点P（m，n）的位置在（ ）
| 1 | ||
|
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
|-5|的相反数是（ ）
| A、5 | ||
| B、-5 | ||
C、-
| ||
D、
|
对于一组统计数据：2，3，5，6，4，4，下列说法错误的是（ ）
| A、众数是4 | B、中位数是4 |
| C、平均数是4 | D、方差是4 |
下列运算正确的是（ ）
| A、x3•x2=x6 |
| B、（x2）3=x5 |
| C、2a-3a=-a |
| D、（x-2）2=x2+4 |
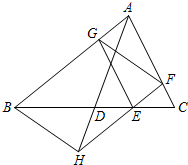已知：如图，在△ABC中，AD是边BC上的中线，点E在线段DC上，EF∥AB交边AC于点F，EG∥AC交边AB于点G，FE的延长线与AD的延长线交于点H．
