题目内容
10.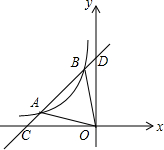 如图,一次函数y1=ax+b的图象与反比例函数y2=$\frac{k}{x}$(x<0)的图象交于A(m,n),B(p,q)两点,与两坐标轴交于C,D两点,连接OA,OB.
如图,一次函数y1=ax+b的图象与反比例函数y2=$\frac{k}{x}$(x<0)的图象交于A(m,n),B(p,q)两点,与两坐标轴交于C,D两点,连接OA,OB.(1)若A,B两点的坐标为A(-3,$\frac{1}{3}$),B(-$\frac{2}{5}$,$\frac{5}{2}$),利用图象求:当y1<y2时,x的取值范围;
(2)当p=-n时,求证:∠AOC=∠BOD.
分析 (1)直接根据两函数图象的交点即可得出结论;
(2)过点A作AE⊥x轴于点E,过点B作BE⊥y轴于点F,由SAS定理得出△OAE≌△OBF,根据全等三角形的性质即可得出结论.
解答  (1)解:由函数图象可知,当y1<y2时,x<-3或-$\frac{2}{5}$<x<0;
(1)解:由函数图象可知,当y1<y2时,x<-3或-$\frac{2}{5}$<x<0;
(2)证明:过点A作AE⊥x轴于点E,过点B作BE⊥y轴于点F,
∵mn=pq=k,p=-n,
∴m=-q,即AE=BF,OE=OF,
在△OAE与△OBF中,
$\left\{\begin{array}{l}AE=BF\\∠AEO=∠BFO\\ OE=OF\end{array}\right.$,
∴△OAE≌△OBF(SAS),
∴∠AOC=∠BOD.
点评 本题考查的是反比例函数综合题,涉及到反比例函数与一次函数的交点问题、全等三角形的判定与性质等知识,根据题意作出辅助线,构造出全等三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1. 如图,AB∥CD,CE平分∠ACD,若∠2=70°,那么∠1=( )
如图,AB∥CD,CE平分∠ACD,若∠2=70°,那么∠1=( )
 如图,AB∥CD,CE平分∠ACD,若∠2=70°,那么∠1=( )
如图,AB∥CD,CE平分∠ACD,若∠2=70°,那么∠1=( )| A. | 70° | B. | 50° | C. | 35° | D. | 25° |
18.以下问题,不适合用普查的是( )
| A. | 了解全班同学每周体育锻炼的时间 | |
| B. | 为了了解“嫦娥二号”卫星零部件的状况 | |
| C. | 学校招聘教师,对应聘人员面试 | |
| D. | 了解一批灯泡的使用寿命 |
15.实数-3的绝对值是( )
| A. | 3 | B. | -3 | C. | 0 | D. | ±$\sqrt{3}$ |
20.下列二次根式中与$\sqrt{3}$是同类二次根式是( )
| A. | $\sqrt{18}$ | B. | $\sqrt{30}$ | C. | $\sqrt{48}$ | D. | $\sqrt{54}$ |
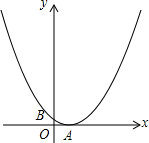 如图,抛物线经过点B(0,1),顶点A在x轴正半轴上,tan∠BAO=$\frac{1}{2}$.
如图,抛物线经过点B(0,1),顶点A在x轴正半轴上,tan∠BAO=$\frac{1}{2}$.