题目内容
16.(1)解不等式$\left\{\begin{array}{l}{x-2≥-3}\\{x-2(x-3)>0}\end{array}\right.$(2)解分式方程$\frac{2}{{x}^{2}-4}$+$\frac{x}{x-2}$=1.
分析 (1)根据解不等式,可得每个不等式的解集,根据不等式组的解集是不等式的解集的公共解,可得答案;
(2)根据等式的性质,可得整式方程,根据解整式方程,可得答案.
解答 解:(1)由x-2≥-3,解得x≥-1,
由x-2(x-3)>0,解得x<6,
不等式组的解集是-1≤x<6;
(2)方程两边都乘以(x2-4),得
2+x(x+2)=x2-4,
解得x=-3,
经检验:x=-3是原分式方程的解.
点评 本题考查了解分式方程,把分式方程转化为整式方程求解.最后注意需验根.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.不等式2x-5<x-1的非负整数解有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,等边△ABC及其内切圆与外接圆构成的图形中,若外接圆的半径为3,则图中阴影部分的面积为3π.
如图,等边△ABC及其内切圆与外接圆构成的图形中,若外接圆的半径为3,则图中阴影部分的面积为3π.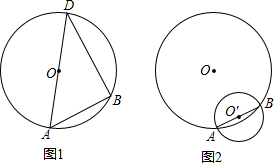 (1)如图1,线段AB的两端点在⊙O上,试用无刻度的直尺过点B作AB的垂线;
(1)如图1,线段AB的两端点在⊙O上,试用无刻度的直尺过点B作AB的垂线;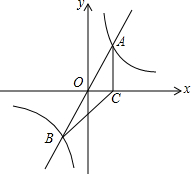 如图,正比例函数y=mx的图象与双曲线y=$\frac{k}{x}$相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC.
如图,正比例函数y=mx的图象与双曲线y=$\frac{k}{x}$相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC.