题目内容
11.观察下列各式,并解答问题;①$\frac{1}{2+\sqrt{2}}$=1-$\frac{\sqrt{2}}{2}$;②$\frac{1}{3\sqrt{2}+2\sqrt{3}}$=$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{3}}{3}$;③$\frac{1}{4\sqrt{3}+3\sqrt{4}}$=$\frac{\sqrt{3}}{3}$-$\frac{\sqrt{4}}{4}$;④$\frac{1}{5\sqrt{4}+4\sqrt{5}}$=$\frac{\sqrt{4}}{4}$-$\frac{\sqrt{5}}{5}$
若n为正整数,用含n的等式来表示你探索的规律.
分析 观察规律后利用规律即可解决问题.
解答 解:根据观察可知:$\frac{1}{(n+1)\sqrt{n}+n\sqrt{n+1}}$=$\frac{\sqrt{n}}{n}$-$\frac{\sqrt{n+1}}{n+1}$.
证明:左边=$\frac{(n+1)\sqrt{n}-n\sqrt{n+1}}{(n+1)^{2}n-{n}^{2}(n+1)}$=$\frac{(n+1)\sqrt{n}-n\sqrt{n+1}}{n(n+1)}$=$\frac{\sqrt{n}}{n}$-$\frac{\sqrt{n+1}}{n+1}$=右边,
故等式成立.
点评 本题考查二次根式的混合运算法则、分母有理化等知识,解题的关键是学会探究规律,利用规律解决问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1. 已知二次函数y=ax2+bx+c(a<0)的图象如图所示,且其顶点的纵坐标为4,则关于x的方程|ax2+bx+c|=5的根的情况是( )
已知二次函数y=ax2+bx+c(a<0)的图象如图所示,且其顶点的纵坐标为4,则关于x的方程|ax2+bx+c|=5的根的情况是( )
 已知二次函数y=ax2+bx+c(a<0)的图象如图所示,且其顶点的纵坐标为4,则关于x的方程|ax2+bx+c|=5的根的情况是( )
已知二次函数y=ax2+bx+c(a<0)的图象如图所示,且其顶点的纵坐标为4,则关于x的方程|ax2+bx+c|=5的根的情况是( )| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 没有实数根 | D. | 有四个实数根 |
19.点P(-3,4)关于原点的对称点是Q(3,m),则m的值是( )
| A. | -4 | B. | 4 | C. | -3 | D. | 3 |
 已知:如图,在?ABCD中,M、N是对角线BD上的两点,且BM=DN.
已知:如图,在?ABCD中,M、N是对角线BD上的两点,且BM=DN.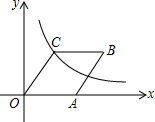 如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴的正半轴上,反比例函数y=$\frac{12}{x}$的图象经过点C(3,m).
如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴的正半轴上,反比例函数y=$\frac{12}{x}$的图象经过点C(3,m).
 如图,一次函数y=-x+4的图象与反比例y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B(b,1)两点,
如图,一次函数y=-x+4的图象与反比例y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B(b,1)两点,