题目内容
1.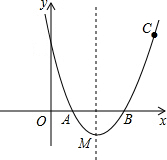 如图,抛物线y=a(x-2)2-1过点C(4,3),交x轴于A,B两点(点A在点B的左侧).
如图,抛物线y=a(x-2)2-1过点C(4,3),交x轴于A,B两点(点A在点B的左侧).(1)求抛物线的解析式,并写出顶点M的坐标;
(2)连接OC,CM,求tan∠OCM的值;
(3)若点P在抛物线的对称轴上,连接BP,CP,BM,当∠CPB=∠PMB时,求点P的坐标.
分析 (1)根据待定系数法,可得函数解析式;根据顶点式解析式,可得顶点坐标;
(2)根据勾股定理及逆定理,可得∠OMC=90°,根据正切函数,可得答案;
(3)根据相似三角形的判定与性质,可得PM的值,可得M点坐标.
解答 解:(1)由抛物线y=a(x-2)2-1过点C(4,3),得
3=a(4-2)2-1,解得a=1,
抛物线的解析式为y=(x-2)2-1,顶点M的坐标为(2,-1);
(2)如图1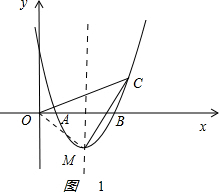 ,
,
连接OM,OC2=32+42=25,OM2=22+12=5,CM2=22+42=20,
∴CM2+OM2=OC2,∴∠OMC=90°,
OM=$\sqrt{5}$,CM=2$\sqrt{5}$,
tan∠OCM=$\frac{OM}{CM}$=$\frac{\sqrt{5}}{2\sqrt{5}}$=$\frac{1}{2}$;
(3)如图2 ,
,
过C作CN⊥对称轴,垂足N在对称轴上,取一点E,使EN=CN=2,连接CE,EM=6.
当y=0时,(x-2)2-1=0,解得的x1=1,x2=3,A(1,0),B(3,0).
∵CN=EN,∴∠CEP=∠PMB=∠CPB=45°,
∵∠EPB=∠EPC+∠CPB=∠PMB+∠PBM,
∴∠EPC=∠PBM
∴△CEP∽△PMB,
∴$\frac{EP}{MB}$=$\frac{CE}{PM}$,解得MB=$\sqrt{2}$,CE=2$\sqrt{2}$,
∴$\frac{6-PM}{\sqrt{2}}$=$\frac{2\sqrt{2}}{PM}$,解得PM=3$±\sqrt{5}$,
P点坐标为(2,2+$\sqrt{5}$)或(2,2-$\sqrt{5}$).
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式;利用相似三角形的判定与性质得出PM的值是解题关键.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案| A. | 1 | B. | -1 | C. | ±1 | D. | 0 |
| A. | x1=x2=0 | B. | x1=2,x2=-2 | C. | x1=0,x2=4 | D. | 没有实数根 |
| A. | $\sqrt{2}$ | B. | $-\sqrt{2}$ | C. | 2 | D. | -2 |
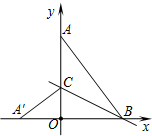 如图,在平面直角坐标系中,点A(0,4)、B(3,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则直线BC的解析式为( )
如图,在平面直角坐标系中,点A(0,4)、B(3,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则直线BC的解析式为( )| A. | y=-$\frac{1}{2}x+\frac{2}{3}$ | B. | y=-x+$\frac{2}{3}$ | C. | y=-$\frac{1}{2}x+\frac{3}{2}$ | D. | y=-2x+$\frac{3}{2}$ |
| A. | 8.0016×106 | B. | 8.0016×107 | C. | 8.0016×108 | D. | 8.0016×109 |