��Ŀ����
10�� ���ı���ABCD�У�AC��BD��AB=13cm��AC=14cm��CD=15cm��BD=28cm����ֱ��BD�ϣ�����P��B����������˶���ͬʱ����һ������Q��D����������˶���
���ı���ABCD�У�AC��BD��AB=13cm��AC=14cm��CD=15cm��BD=28cm����ֱ��BD�ϣ�����P��B����������˶���ͬʱ����һ������Q��D����������˶�����1����֪������P��Q���ٶȷֱ���1cm/s��2cm/s�����˶��ʱ�����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ���д�������̣�
��2������A��C��P��Q�ĵ�Ϊ������ı����Ǿ��Σ���P��Q�����˶��ٶ�֮�ȣ�����д�����̣�VP��VQ=5��9��19��23��
��3������A��C��P��Q�ĵ�Ϊ������ı��������Σ���P��Q�����˶��ٶ�֮�ȣ�����д�����̣�������Բ�����VP��VQ=��5+2$\sqrt{13}$������9-2$\sqrt{13}$����VP��VQ=��19+2$\sqrt{13}$������23-2$\sqrt{13}$������
���� ��1����ͼ1�У���AC=PQʱ����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ��г����̼��ɽ�����⣮
��2����ͼ2�У���AE��CD��BD��E����AH��BD��D��CF��BD��F���������������ۼ��ɣ�
��3����ͼ3�У���AE��CD��BD��E����AH��BD��D��CF��BD��F��AP=AC=PQʱ���ı���APQC�����Σ��ɣ�2����֪��AE=CD=15��AD=12��BD=5�������������г����̽����
��� �⣺��1����ͼ1�У���AC=PQʱ����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���
�����⣺28-t-2t=14��2t+t-28=14��
��t=$\frac{14}{3}$��14��
���˶�$\frac{14}{3}$ ��14��ʱ�����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ�
��2����ͼ2�У���AE��CD��BD��E����AH��BD��D��CF��BD��F��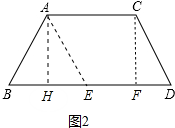
��AC��ED��AE��CD��
���ı���AEDC��ƽ���ı��Σ�
��AE=CD=15����BDΪx����AB2-BH2=AE2-HE2��
��132-x2=152-��14-x��2��
���x=5��
��AH=12��BH=5��HE=9��
��RT��CFD��DF=$\sqrt{C{D}^{2}-C{F}^{2}}$=9��
�ٵ���P�˶�����D����Q�˶�����Fʱ����A��C��P��Q�ĵ�Ϊ������ı����Ǿ��Σ�
��VP��VQ=BH��DF=5��9��
�ڵ���P�˶�����F����Q�˶�����Dʱ����A��C��P��Q�ĵ�Ϊ������ı����Ǿ��Σ�
��VP��VQ=BF��DH=19��23��
�ʴ𰸷ֱ�Ϊ5��9��19��23��
��3����ͼ3�У���AE��CD��BD��E����AH��BD��D��CF��BD��F��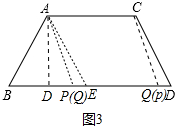
��AP=AC=PQʱ���ı���APQC�����Σ��ɣ�2����֪��AE=CD=15��AD=12��BD=5��
��AC=AP=14��
��DP=$\sqrt{1{4}^{2}-1{2}^{2}}$=2$\sqrt{13}$��
��BP=5+2$\sqrt{13}$��DQ=14-5-2$\sqrt{2}$=9-2$\sqrt{3}$��
��VP��VQ=BP��DQ=��5+2$\sqrt{13}$������9-2$\sqrt{13}$����VP��VQ=��19+2$\sqrt{13}$������23-2$\sqrt{13}$����
�ʴ�Ϊ=��5+2$\sqrt{13}$������9-2$\sqrt{13}$����VP��VQ=��19+2$\sqrt{13}$������23-2$\sqrt{13}$����
���� ���⿼���ı����ۺ��⡢ƽ���ı��ε����ʡ����ɶ�����֪ʶ���ˡ���Ĺؼ������Ӹ����߹������������ν�����⣬�����п��������ͣ�

 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�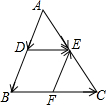 ��ͼ����֪�ڡ�ABC�У���D��E��F�ֱ���AB��AC��BC���е㣮���н��۲���ȷ���ǣ�������
��ͼ����֪�ڡ�ABC�У���D��E��F�ֱ���AB��AC��BC���е㣮���н��۲���ȷ���ǣ�������| A�� | $\overrightarrow{DE}$��$\overrightarrow{BC}$ | B�� | $\overrightarrow{AD}-\overrightarrow{AE}=\overrightarrow{DE}$ | C�� | $\overrightarrow{DB}$=$-\overrightarrow{FE}$ | D�� | $\overrightarrow{DB}+\overrightarrow{DE}+\overrightarrow{FE}=\overrightarrow{DE}$ |
| A�� | �������ֱ�߶��������ֱ��ƽ�У���ô������ֱ��Ҳ����ƽ�� | |
| B�� | ��ͬһƽ���ڣ���һ������ֻ��һ��ֱ������ֱ֪�ߴ�ֱ | |
| C�� | ����ֱ�߱�������ֱ�����أ�ͬ���ڽǻ��� | |
| D�� | ��ֱ��ƽ�У��ڴ������ |
 ��ͼ����M��N�ֱ��ڡ�AOB�ı�OA��OB�ϣ���OM=ON��
��ͼ����M��N�ֱ��ڡ�AOB�ı�OA��OB�ϣ���OM=ON�� ��ͼ��AC�Ǿ���ABCD�ĶԽ��ߣ�DE��AC�ڵ�E��
��ͼ��AC�Ǿ���ABCD�ĶԽ��ߣ�DE��AC�ڵ�E��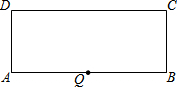 ����ABCD�У�AB=10��BC=4��QΪAB�ߵ��е㣬PΪCD���ϵĶ��㣬�ҡ�AQP������Ϊ5�ĵ��������Σ���CP�ij�Ϊ2��7��8��
����ABCD�У�AB=10��BC=4��QΪAB�ߵ��е㣬PΪCD���ϵĶ��㣬�ҡ�AQP������Ϊ5�ĵ��������Σ���CP�ij�Ϊ2��7��8��