题目内容
2. 如图,已知⊙O的半径是6cm,弦CB=$6\sqrt{3}$cm,OD⊥BC,垂足为D,求∠COB.
如图,已知⊙O的半径是6cm,弦CB=$6\sqrt{3}$cm,OD⊥BC,垂足为D,求∠COB.
分析 根据垂径定理求出CD的长,根据正弦的概念求出∠COD的度数,得到答案.
解答 解:∵OD⊥BC,CB=$6\sqrt{3}$,
∴CD=3$\sqrt{3}$,又OD⊥BC,OC=6,
∴sin∠COD=$\frac{CD}{OC}$=$\frac{\sqrt{3}}{2}$,
∴∠COD=60°,
∴∠COB=120°.
点评 本题考查的是垂径定理的应用、锐角三角函数的概念,掌握垂直于弦的直径平分弦是解题的关键.

练习册系列答案
相关题目
7.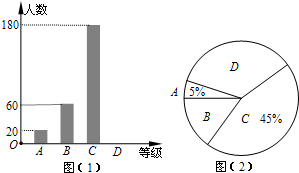 某报社为了解宿迁市民对大范围雾霾天气的成因、影响以及应对措施的看法,做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.请结合统计图表,回答下列问题.
某报社为了解宿迁市民对大范围雾霾天气的成因、影响以及应对措施的看法,做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.请结合统计图表,回答下列问题.
(1)本次参与调查的市民共有400人,m=15%;
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是126度;
(3)请将图1的条形统计图补充完整;
(4)根据调查结果.学校准备开展关于雾霾知识竞赛,某班要从小明和小刚中选一人参加,现设计了如下游戏来确定:在一个不透明的袋中装有1个红球和2个白球,它们除了颜色外都相同,小明先从袋中随机摸出一个球,小刚再从剩下的两个球中随机摸出一个球,若小明和小刚摸出的两个球颜色相同,则小明去;否则小刚去.现在,小明同学摸出了一个白球,则小明参加竞赛的概率为多少?
 某报社为了解宿迁市民对大范围雾霾天气的成因、影响以及应对措施的看法,做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.请结合统计图表,回答下列问题.
某报社为了解宿迁市民对大范围雾霾天气的成因、影响以及应对措施的看法,做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.请结合统计图表,回答下列问题.| 对雾霾的了解程度 | 百分比 |
| A.非常了解 | 5% |
| B.比较了解 | m |
| C.基本了解 | 45% |
| D.不了解 | n |
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是126度;
(3)请将图1的条形统计图补充完整;
(4)根据调查结果.学校准备开展关于雾霾知识竞赛,某班要从小明和小刚中选一人参加,现设计了如下游戏来确定:在一个不透明的袋中装有1个红球和2个白球,它们除了颜色外都相同,小明先从袋中随机摸出一个球,小刚再从剩下的两个球中随机摸出一个球,若小明和小刚摸出的两个球颜色相同,则小明去;否则小刚去.现在,小明同学摸出了一个白球,则小明参加竞赛的概率为多少?
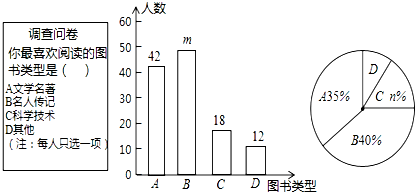
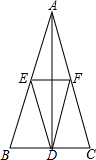 如图.在△ABC中,AB=AC,AD平分∠BAC交BC于点D,E,F分别是AB,AC的中点,△DEF是等腰三角形吗?请说明理由.
如图.在△ABC中,AB=AC,AD平分∠BAC交BC于点D,E,F分别是AB,AC的中点,△DEF是等腰三角形吗?请说明理由. 如图所示,AB,BC,AC都是⊙O的弦,且∠AOB=∠BOC.
如图所示,AB,BC,AC都是⊙O的弦,且∠AOB=∠BOC.