题目内容
17.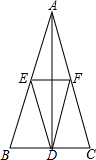 如图.在△ABC中,AB=AC,AD平分∠BAC交BC于点D,E,F分别是AB,AC的中点,△DEF是等腰三角形吗?请说明理由.
如图.在△ABC中,AB=AC,AD平分∠BAC交BC于点D,E,F分别是AB,AC的中点,△DEF是等腰三角形吗?请说明理由.
分析 由等腰△ABC,根据等边对等角,得到∠B=∠C,由平行线的性质得到角相等,由等量代换得到∠AEF=∠AFE,证得AE=AF,由等腰三角形的三线合一的性质证得AD是EF的中垂线,由中垂线的性质得到结论.
解答 解:△DEF是等腰三角形,
∵AB=AC,
∴∠B=∠C,
∵E,F分别是AB,AC的中点,
∴EF∥BC,
∴∠AEF=∠B,∠AFE=∠C,
∴∠AEF=∠AFE,
∴AE=AF,
∵AB=AC,AD平分∠BAC交BC于点D,
∴AD⊥BC,
∴AD⊥EF,
∴AD垂直平分EF,
∴DE=DF,
∴△DEF是等腰三角形.
点评 本题主要考查了平行线的性质,等腰三角形的判定,线段垂直平分线的判定和性质,解决本题的关键是熟记等腰三角形的判定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.某商场对上周女装的销售情况进行了统计,如下表:
经理决定本周进女装时多进L号,可用来解释这一现象的统计量是( )
| 尺寸 | S | M | L | XL | XXL |
| 数量(件) | 50 | 110 | 150 | 80 | 70 |
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
9.对于二次函数y=(x-1)2+2的图象,下列说法正确的是( )
| A. | 开口向下 | B. | 顶点坐标是(1,2) | C. | 对称轴是x=-1 | D. | 有最大值是2 |
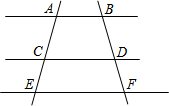 如图,直线AB∥CD∥EF,若AC=3,CE=4,则$\frac{BD}{BF}$的值是$\frac{3}{7}$.
如图,直线AB∥CD∥EF,若AC=3,CE=4,则$\frac{BD}{BF}$的值是$\frac{3}{7}$. 如图,已知⊙O的半径是6cm,弦CB=$6\sqrt{3}$cm,OD⊥BC,垂足为D,求∠COB.
如图,已知⊙O的半径是6cm,弦CB=$6\sqrt{3}$cm,OD⊥BC,垂足为D,求∠COB. 在高度为2.8m的一面墙上,准备开凿一个矩形窗户,现用9.5m长的铝合金条制成如图所示的窗框,设宽为xm,窗户的透光面积为ym2
在高度为2.8m的一面墙上,准备开凿一个矩形窗户,现用9.5m长的铝合金条制成如图所示的窗框,设宽为xm,窗户的透光面积为ym2