题目内容
10.如果3m-2n=0(m,n≠0),那么$\frac{n}{m}$=$\frac{3}{2}$,$\frac{m+n}{m}$=$\frac{5}{2}$,$\frac{m+n}{n}$=$\frac{5}{3}$.分析 根据等式的性质,可得n:m,根据和比性质,可得答案;根据等式的性质,可得m:n,根据和比性质,可得答案.
解答 解:由3m-2n=0,得
3m=2n,
$\frac{n}{m}$=$\frac{3}{2}$,
$\frac{m+n}{m}$=$\frac{3+2}{2}$=$\frac{5}{2}$;
3m=2n,
$\frac{m}{n}$=$\frac{2}{3}$,$\frac{m+n}{n}$=$\frac{2+3}{3}$=$\frac{5}{3}$,
故答案为:$\frac{2}{3}$,$\frac{5}{2}$,$\frac{5}{3}$.
点评 本题考查了比例的性质,利用了等式的性质,和比性质:$\frac{a}{b}$=$\frac{c}{d}$⇒$\frac{a+b}{b}$=$\frac{c+d}{d}$.

练习册系列答案
相关题目
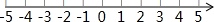 结合数轴与绝对值的知识回答下列问题:
结合数轴与绝对值的知识回答下列问题: 如图,已知⊙O的半径是6cm,弦CB=$6\sqrt{3}$cm,OD⊥BC,垂足为D,求∠COB.
如图,已知⊙O的半径是6cm,弦CB=$6\sqrt{3}$cm,OD⊥BC,垂足为D,求∠COB.