题目内容
10.已知关于x的一元二次方程x2+3x+k=0有实数根,则下列四个数中,满足条件的k值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据方程有实数根结合根的判别式可得出关于k的一元一次不等式9-4k≥0,解不等式得出k的取值范围,再结合四个选项即可得出结论.
解答 解:∵方程x2+3x+k=0有实数根,
∴△=32-4×1×k=9-4k≥0,
解得:k≤$\frac{9}{4}$.
在A、B、C、D选项中只有A中的2符合条件.
故选A.
点评 本题考查了根的判别式以及解一元一次不等式,解题的关键是得出关于k的一元一次不等式9-4k≥0.本题属于基础题,难度不大,解决该题型题目时,根据方程根的情况结合根的判别式得出不等式是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.下列运算中正确的是( )
| A. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | B. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{5}$ | ||
| C. | $\sqrt{{5}^{2}-{3}^{2}}$=$\sqrt{{5}^{2}}$-$\sqrt{{3}^{2}}$=5-3=2 | D. | $\sqrt{3}$-$\sqrt{12}$=-$\sqrt{3}$ |
18.下列计算正确的是( )
| A. | x3÷x=x3 | B. | x3•x2=x5 | C. | (x3)2=x5 | D. | (2x)3=6x3 |
15.不等式3x+2<2x+3的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
19.若一元二次方程-3x2+6x+m=0有实根,则m的取值范围是( )
| A. | m≤-3 | B. | m<-3 | C. | m≥-3 | D. | m>-3 |
19.化简$\frac{16-{a}^{2}}{{a}^{2}+4a+4}$÷$\frac{a-4}{2a+4}$•$\frac{a-2}{a+4}$,其结果是( )
| A. | -2 | B. | 2 | C. | -$\frac{2(a-2)}{a+2}$ | D. | $\frac{2}{(a+2)^{2}}$ |
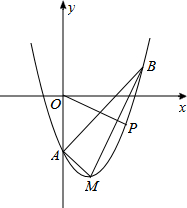 如图,在平面直角坐标系xOy中,顶点为M的抛物线是由抛物线y=x2-3向右平移一个单位后得到的,它与y轴负半轴交于点A,点B在该抛物线上,且横坐标为3.
如图,在平面直角坐标系xOy中,顶点为M的抛物线是由抛物线y=x2-3向右平移一个单位后得到的,它与y轴负半轴交于点A,点B在该抛物线上,且横坐标为3.