题目内容
19.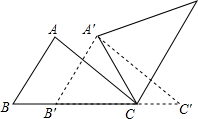 如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离为2,旋转角的度数为60°.
如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离为2,旋转角的度数为60°.
分析 根据平移和旋转的性质得到三角形全等,进而解答即可.
解答 解:∵将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,
∴△ABC≌△A'B'C',
∴AB=A'B'=A'C,
∴△A'B'C是等边三角形,
∴∠A'CB'=60°,B'C=AB=4,
∴BB'=6-4=2,旋转角的度数为60°,
故答案为:2,60°;
点评 本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
9.在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
| A. | AB∥DC,AD=BC | B. | AB=DC,AD=BC | C. | AO=CO,BO=DO | D. | AB∥DC,AD∥BC |
11.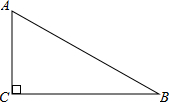 如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( )
 如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( )| A. | $\frac{4\sqrt{3}}{3}$ | B. | 4 | C. | 8$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
 将矩形ABCD折叠使点A,C重合,折痕交BC于点E,交AD于点F,可以得到四边形AECF是一个菱形,若AB=4,BC=8,求菱形AECF的面积.
将矩形ABCD折叠使点A,C重合,折痕交BC于点E,交AD于点F,可以得到四边形AECF是一个菱形,若AB=4,BC=8,求菱形AECF的面积. 已知任意三角形的三边长,如何求三角形面积?
已知任意三角形的三边长,如何求三角形面积? 如图,已知正方形ABCD的对角线长为$\sqrt{2}$,将正方形ABCD沿直线EF折叠,则图中阴影部分的周长为4.
如图,已知正方形ABCD的对角线长为$\sqrt{2}$,将正方形ABCD沿直线EF折叠,则图中阴影部分的周长为4.