题目内容
4.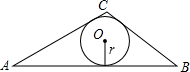 已知任意三角形的三边长,如何求三角形面积?
已知任意三角形的三边长,如何求三角形面积?古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式--海伦公式S=$\sqrt{p(p-a)(p-b)(p-c)}$(其中a,b,c是三角形的三边长,p=$\frac{a+b+c}{2}$,S为三角形的面积),并给出了证明
例如:在△ABC中,a=3,b=4,c=5,那么它的面积可以这样计算:
∵a=3,b=4,c=5
∴p=$\frac{a+b+c}{2}$=6
∴S=$\sqrt{p(p-a)(p-b)(p-c)}$=$\sqrt{6×3×2×1}$=6
事实上,对于已知三角形的三边长求三角形面积的问题,还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决.
如图,在△ABC中,BC=5,AC=6,AB=9
(1)用海伦公式求△ABC的面积;
(2)求△ABC的内切圆半径r.
分析 (1)先根据BC、AC、AB的长求出P,再代入到公式S=$\sqrt{p(p-a)(p-b)(p-c)}$即可求得S的值;
(2)根据公式S=$\frac{1}{2}$r(AC+BC+AB),代入可得关于r的方程,解方程得r的值.
解答 解:(1)∵BC=5,AC=6,AB=9,
∴p=$\frac{BC+AC+AB}{2}$=$\frac{5+6+9}{2}$=10,
∴S=$\sqrt{p(p-a)(p-b)(p-c)}$=$\sqrt{10×5×4×1}$=10$\sqrt{2}$;
故△ABC的面积10$\sqrt{2}$;
(2)∵S=$\frac{1}{2}$r(AC+BC+AB),
∴10$\sqrt{2}$=$\frac{1}{2}$r(5+6+9),
解得:r=$\sqrt{2}$,
故△ABC的内切圆半径r=$\sqrt{2}$.
点评 本题主要三角形的内切圆与内心、二次根式的应用,熟练掌握三角形的面积与内切圆半径间的公式是解题的关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
15.在平面直角坐标系中,点(5,3)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
16.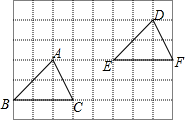 如图,△ABC经过怎样的平移得到△DEF( )
如图,△ABC经过怎样的平移得到△DEF( )
 如图,△ABC经过怎样的平移得到△DEF( )
如图,△ABC经过怎样的平移得到△DEF( )| A. | 把△ABC向左平移5个单位,再向下平移2个单位 | |
| B. | 把△ABC向右平移5个单位,再向下平移2个单位 | |
| C. | 把△ABC向右平移5个单位,再向上平移2个单位 | |
| D. | 把△ABC向左平移5个单位,再向上平移两个单位 |
14.下列命题中是假命题的是( )
| A. | 平行四边形的对角线互相平分 | B. | 等腰梯形的对角线相等 | ||
| C. | 对角线互相垂直的四边形是菱形 | D. | 对角线相等的菱形是正方形 |
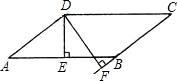 如图所示,?ABCD的周长是10$\sqrt{3}$+6$\sqrt{2}$,AB的长是5$\sqrt{3}$,DE⊥AB于E,DF⊥CB交CB的延长线于点F,DE的长是3,则DF的长为$\frac{5\sqrt{6}}{2}$.
如图所示,?ABCD的周长是10$\sqrt{3}$+6$\sqrt{2}$,AB的长是5$\sqrt{3}$,DE⊥AB于E,DF⊥CB交CB的延长线于点F,DE的长是3,则DF的长为$\frac{5\sqrt{6}}{2}$.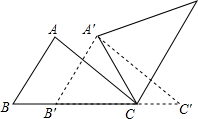 如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离为2,旋转角的度数为60°.
如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离为2,旋转角的度数为60°.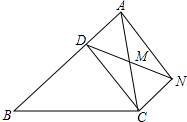 已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,若MA=MC,∠BAN=90°,求证:四边形ADCN是矩形.
已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,若MA=MC,∠BAN=90°,求证:四边形ADCN是矩形.