题目内容
8. 如图,已知正方形ABCD的对角线长为$\sqrt{2}$,将正方形ABCD沿直线EF折叠,则图中阴影部分的周长为4.
如图,已知正方形ABCD的对角线长为$\sqrt{2}$,将正方形ABCD沿直线EF折叠,则图中阴影部分的周长为4.
分析 根据正方形对角线的长,求出正方形的边长,由图形翻折变换的性质可知AD=A′D′,A′H=AH,D′G=DG,由阴影部分的周长=A′D′+A′H+BH+BC+CG+D′G即可得出结论.
解答  解:∵正方形ABCD的对角线长为$\sqrt{2}$,
解:∵正方形ABCD的对角线长为$\sqrt{2}$,
∴正方形ABCD的边长为1,
由翻折变换的性质可知AD=A′D′,A′H=AH,D′G=DG,
阴影部分的周长=A′D′+(A′H+BH)+BC+(CG+D′G)=AD+AB+BC+CD=1×4=4.
故答案为:4.
点评 本题考查的是翻折变换的性质,即折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.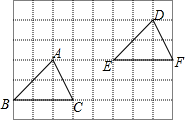 如图,△ABC经过怎样的平移得到△DEF( )
如图,△ABC经过怎样的平移得到△DEF( )
 如图,△ABC经过怎样的平移得到△DEF( )
如图,△ABC经过怎样的平移得到△DEF( )| A. | 把△ABC向左平移5个单位,再向下平移2个单位 | |
| B. | 把△ABC向右平移5个单位,再向下平移2个单位 | |
| C. | 把△ABC向右平移5个单位,再向上平移2个单位 | |
| D. | 把△ABC向左平移5个单位,再向上平移两个单位 |
17.若$\sqrt{{a}^{2}}$=-a成立,则a满足的条件是( )
| A. | a<0 | B. | a≤0 | C. | a>0 | D. | a≥0 |
18.为了解2016年泰兴市八年级学生的视力情况,从中随机调查了500名学生的视力情况.下列说法正确的是( )
| A. | 2016年泰兴市八年级学生是总体 | |
| B. | 每一名八年级学生是个体 | |
| C. | 500名八年级学生是总体的一个样本 | |
| D. | 样本容量是500 |
 请用割补法作图,将一个锐角三角形经过一次或两次分割后,重新拼成一个与原三角形面积相等的平行四边形(只要求用一种方法画出图形,把相等的线段作相同的标记).
请用割补法作图,将一个锐角三角形经过一次或两次分割后,重新拼成一个与原三角形面积相等的平行四边形(只要求用一种方法画出图形,把相等的线段作相同的标记).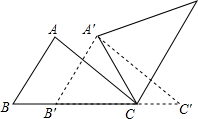 如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离为2,旋转角的度数为60°.
如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离为2,旋转角的度数为60°.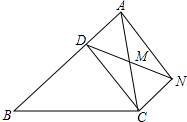 已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,若MA=MC,∠BAN=90°,求证:四边形ADCN是矩形.
已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,若MA=MC,∠BAN=90°,求证:四边形ADCN是矩形.