题目内容
11.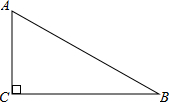 如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( )| A. | $\frac{4\sqrt{3}}{3}$ | B. | 4 | C. | 8$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
分析 根据cosB=$\frac{BC}{AB}$及特殊角的三角函数值解题即可.
解答 解:∵在Rt△ABC中,∠C=90°,∠B=30°,AB=8,
cosB=$\frac{BC}{AB}$,
即cos30°=$\frac{BC}{8}$,
∴BC=8×$\frac{\sqrt{3}}{2}$=4$\sqrt{3}$;
故选:D.
点评 本题考查了三角函数的定义及特殊角的三角函数值,是基础知识,需要熟练掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.不等式组$\left\{\begin{array}{l}{\frac{1}{3}x+1>0}\\{3-x≥2}\end{array}\right.$的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. | 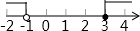 |
6.下列计算正确的是( )
| A. | ($\sqrt{2}$)2=2 | B. | $\sqrt{3}$-$\sqrt{2}$=1 | C. | $\sqrt{6}$÷$\sqrt{2}$=3 | D. | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{5}$ |
16.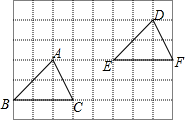 如图,△ABC经过怎样的平移得到△DEF( )
如图,△ABC经过怎样的平移得到△DEF( )
 如图,△ABC经过怎样的平移得到△DEF( )
如图,△ABC经过怎样的平移得到△DEF( )| A. | 把△ABC向左平移5个单位,再向下平移2个单位 | |
| B. | 把△ABC向右平移5个单位,再向下平移2个单位 | |
| C. | 把△ABC向右平移5个单位,再向上平移2个单位 | |
| D. | 把△ABC向左平移5个单位,再向上平移两个单位 |
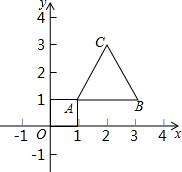 如图,等边三角形的顶点A(1,1)、B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次変换,如果这样连续经过2016次变换后,等边△ABC的顶点C的坐标为(-2014,$\sqrt{3}$+1).
如图,等边三角形的顶点A(1,1)、B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次変换,如果这样连续经过2016次变换后,等边△ABC的顶点C的坐标为(-2014,$\sqrt{3}$+1).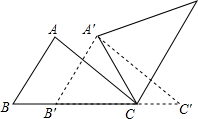 如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离为2,旋转角的度数为60°.
如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离为2,旋转角的度数为60°.