题目内容
12. 如图,∠ABC=50°,∠ACB=60°,∠ABC与∠ACB的平分线交于点O,过O作DE∥BC,交AB、AC于点D、E,求∠BOC的度数.
如图,∠ABC=50°,∠ACB=60°,∠ABC与∠ACB的平分线交于点O,过O作DE∥BC,交AB、AC于点D、E,求∠BOC的度数.
分析 根据角平分线的定义求出∠OBC、∠OCB,再根据三角形的内角和定理列式计算即可得解.
解答 解:∵∠ABC、∠ACB的平分线交于点O,
∴∠OBC=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×50°=25°,
∠OCB=$\frac{1}{2}$∠ACB=$\frac{1}{2}$×60°=30°,
在△OBC中,∠BOC=180°-∠OBC-∠OCB=180°-25°-30°=125°.
点评 本题考查了三角形的内角和定理,角平分线的定义,是基础题,熟记概念并准确识图是解题的关键.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案
相关题目
4.平方根与立方根相等的数是( )
| A. | 1 | B. | 0 | C. | 1和0 | D. | 0,1 |
2.下列图形中,既是中心对称图形又是有且只有两条对称轴的对称图形是( )
| A. | 正三角形 | B. | 正方形 | C. | 圆 | D. | 矩形 |
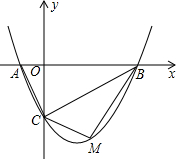 如图,二次函数y=ax2-$\frac{3}{2}$x+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知点A(-1,0),点C(0,-2).
如图,二次函数y=ax2-$\frac{3}{2}$x+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知点A(-1,0),点C(0,-2).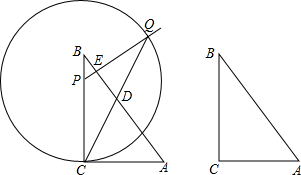

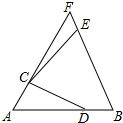 如图,等边△ABF中,点C,D分别在AF、AB上,线段CD绕点C逆时针旋转60°到线段CE,点E恰好落在BF上.
如图,等边△ABF中,点C,D分别在AF、AB上,线段CD绕点C逆时针旋转60°到线段CE,点E恰好落在BF上. 已知:如图,矩形ABCD的对角线相交于点O,
已知:如图,矩形ABCD的对角线相交于点O,