题目内容
11.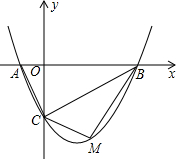 如图,二次函数y=ax2-$\frac{3}{2}$x+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知点A(-1,0),点C(0,-2).
如图,二次函数y=ax2-$\frac{3}{2}$x+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知点A(-1,0),点C(0,-2).(1)求抛物线的函数解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上的一个动点,求面积的最大值以及此时点M的坐标.
分析 (1)将点A、点C的坐标代入抛物线的解析式得到关于a、c的二元一次方程组,求得a、c的值,从而可求得抛物线的解析式;
(2)先求得点B的坐标,然后求得AB、AC、BC的长,依据勾股定理的逆定理可证明△ABC为直角三角形,△ABC的外心为AB的中,从而可求得为外接圆圆心的坐标;
(3)过点M作ME⊥AB,垂足为E,ME交BC于点D.先求得直线BC的解析式,设点M的坐标为(a,$\frac{1}{2}$a2-$\frac{3}{2}$a-2).则点D的坐标为(a,$\frac{1}{2}$a-2),用含a的式子表示出△BCM的面积,依据配方法可求得△CBM面积的最大值以及此时点M的坐标.
解答 解:(1)∵将A(-1,0)、点C(0,-2)代入抛物线的解析式得:$\left\{\begin{array}{l}{a+\frac{3}{2}+c=0}\\{c=-2}\end{array}\right.$,解得;$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{c=-2}\end{array}\right.$,
∴抛物线的解析式为y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2.
(2)令y=0得:$\frac{1}{2}$x2-$\frac{3}{2}$x-2=0,解得:x1=-1,x2=4.
∴B(4,0).
∴AB=5.
∴AB2=25.
在Rt△AOC中,由勾股定理得:AC2=AO2+OC2=5,在Rt△OBC中,由勾股定理得;CB2=OC2+OB2=20.
∴AB2=AC2+BC2.
∴△ABC为直角三角形.
∴△ABC的外接圆的圆心为AB的中点,且坐标为.
∴△ABC的外接圆的圆心为AB的中点,且坐标为($\frac{3}{2}$,0).
(3)如图所示:过点M作ME⊥AB,垂足为E,ME交BC于点D.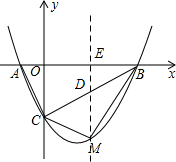
设BC的解析式为y=kx+b.
∵将B(4,0),C(0,-2)代入得:$\left\{\begin{array}{l}{4k+b=0}\\{b=-2}\end{array}\right.$,解得:k=$\frac{1}{2}$,b=-2,
∴抛物线的解析式为y=$\frac{1}{2}x-2$.
设点M的坐标为(a,$\frac{1}{2}$a2-$\frac{3}{2}$a-2).则点D的坐标为(a,$\frac{1}{2}$a-2).
∵MD=EM-ED,
∴MD=$\frac{1}{2}$a-2-($\frac{1}{2}$a2-$\frac{3}{2}$a-2)=-$\frac{1}{2}$a2+2a.
∴S△CBM=$\frac{1}{2}$OB•DM=-a2+4a=-(a-2)2+4.
∴当a=2时,△CBM的面积有最大值,△CBM的面积的最大值为4.
∵将a=2代入y=$\frac{1}{2}$a2-$\frac{3}{2}$a-2得:y=-3,
∴点M的坐标为(2,-3).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数、二次函数的解析式、勾股定理和勾股定理的逆定理、配方法求二次函数的最值,列出△BCM的面积与a的函数关系式是解题的关键.

| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
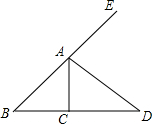 如图,AD是∠CAE的平分线,∠B=35°,∠DAE=60°,则∠ACD=( )
如图,AD是∠CAE的平分线,∠B=35°,∠DAE=60°,则∠ACD=( )| A. | 25° | B. | 85° | C. | 60° | D. | 95° |
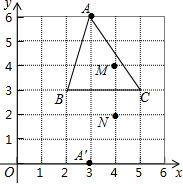 如图所示,△ABC和△A′BC存在着某种对应关系(它们关于BC对称),其中A的对应点是A′,A(3,6),A′(3,0),△ABC内部的点M(4,4)的对应点是N(4,2).
如图所示,△ABC和△A′BC存在着某种对应关系(它们关于BC对称),其中A的对应点是A′,A(3,6),A′(3,0),△ABC内部的点M(4,4)的对应点是N(4,2).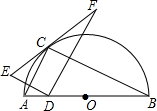 如图,点C在以AB为直径的半圆上,AB=4,∠CBA=30°,点D在AO上运动,点E与点D关于AC对称:DF⊥DE于点D,并交EC的延长线于点F,下列结论:
如图,点C在以AB为直径的半圆上,AB=4,∠CBA=30°,点D在AO上运动,点E与点D关于AC对称:DF⊥DE于点D,并交EC的延长线于点F,下列结论: 如图,∠ABC=50°,∠ACB=60°,∠ABC与∠ACB的平分线交于点O,过O作DE∥BC,交AB、AC于点D、E,求∠BOC的度数.
如图,∠ABC=50°,∠ACB=60°,∠ABC与∠ACB的平分线交于点O,过O作DE∥BC,交AB、AC于点D、E,求∠BOC的度数.