题目内容
17.解方程组(1)$\left\{\begin{array}{l}{x-3y=5①}\\{2x+y=5②}\end{array}\right.$
(2)$\left\{\begin{array}{l}{2x+2y=8}\\{2x-2y=4}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)①+②×3得:7x=20,即x=$\frac{20}{7}$,
②-①×2得:7y=-5,即y=-$\frac{5}{7}$,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{20}{7}}\\{y=-\frac{5}{7}}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{2x+2y=8①}\\{2x-2y=4②}\end{array}\right.$,
①+②得:4x=12,即x=3,
①-②得:4y=4,即y=1,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
16.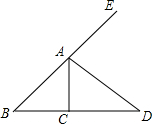 如图,AD是∠CAE的平分线,∠B=35°,∠DAE=60°,则∠ACD=( )
如图,AD是∠CAE的平分线,∠B=35°,∠DAE=60°,则∠ACD=( )
 如图,AD是∠CAE的平分线,∠B=35°,∠DAE=60°,则∠ACD=( )
如图,AD是∠CAE的平分线,∠B=35°,∠DAE=60°,则∠ACD=( )| A. | 25° | B. | 85° | C. | 60° | D. | 95° |
2.盐城市2015年初中毕业生人数达10.1万.数据10.1万用科学记数法表示为( )
| A. | 1.01×10 | B. | 10.1×104 | C. | 1.01×105 | D. | 0.101×106 |
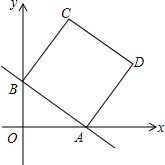 如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+b分别与x轴、y轴交于点A、B,且点A的坐标为(4,0),四边形ABCD是正方形.
如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+b分别与x轴、y轴交于点A、B,且点A的坐标为(4,0),四边形ABCD是正方形. 如图,∠ABC=50°,∠ACB=60°,∠ABC与∠ACB的平分线交于点O,过O作DE∥BC,交AB、AC于点D、E,求∠BOC的度数.
如图,∠ABC=50°,∠ACB=60°,∠ABC与∠ACB的平分线交于点O,过O作DE∥BC,交AB、AC于点D、E,求∠BOC的度数. 如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:
如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论: