题目内容
1. 已知:如图,矩形ABCD的对角线相交于点O,
已知:如图,矩形ABCD的对角线相交于点O,(1)若AB=2,∠AOD=120°,求对角线AC的长;
(2)若AC=2AB.求证:△AOB是等边三角形.
分析 (1)根据矩形的对角线互相平分且相等可得OA=OB=$\frac{1}{2}$AC,根据邻补角的定义求出∠AOB,然后判断出△AOB是等边三角形,根据等边三角形的性质可得OA=AB,然后求解即可;
(2)由矩形的性质易得:AC=2AO=2BO,又因为AC=2AB,所以AO=BO=AB,进而可证明△AOB是等边三角形.
解答 (1)解:∵矩形ABCD的两条对角线交于点O,
∴OA=OB=$\frac{1}{2}$AC,
∵∠AOD=120°,
∴∠AOB=180°-∠AOD=180°-120°=60°,
∴△AOB是等边三角形,
∴OA=AB=2,
∴AC=2OA=2×2=4;
(2)证明:∵四边形ABCD是矩形,
∴AC=BD,AO=CO=$\frac{1}{2}$AC,BO=DO=$\frac{1}{2}$BD,
∴AO=BO=$\frac{1}{2}$AC,
∵AC=2AB,
∴AO=BO=AB,
∴△AOB是等边三角形.
点评 本题考查了矩形的性质,等边三角形的判定与性质,熟记矩形的对角线互相平分且相等是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
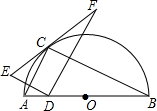 如图,点C在以AB为直径的半圆上,AB=4,∠CBA=30°,点D在AO上运动,点E与点D关于AC对称:DF⊥DE于点D,并交EC的延长线于点F,下列结论:
如图,点C在以AB为直径的半圆上,AB=4,∠CBA=30°,点D在AO上运动,点E与点D关于AC对称:DF⊥DE于点D,并交EC的延长线于点F,下列结论: 如图,∠ABC=50°,∠ACB=60°,∠ABC与∠ACB的平分线交于点O,过O作DE∥BC,交AB、AC于点D、E,求∠BOC的度数.
如图,∠ABC=50°,∠ACB=60°,∠ABC与∠ACB的平分线交于点O,过O作DE∥BC,交AB、AC于点D、E,求∠BOC的度数. 如图,已知MN⊥AB于P,MN⊥CD于Q,∠2=70°,求∠1.
如图,已知MN⊥AB于P,MN⊥CD于Q,∠2=70°,求∠1. 如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:
如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论: