题目内容
4.两个正六边形,小正六边形的边长为3cm,大正六边形的周长为24cm.(1)这两个正六边形是否相似?为什么?
(2)这两个正六边形中最长对角线的比是多少?
分析 (1)根据相似多边形的判定定理判断即可;
(2)分别求出两个正六边形的对角线,然后求出它们的比即可.
解答 解:(1)相似,
∵小正六边形的边长为3cm,
∵大正六边形的周长为24cm.
∴大正六边形的边长为4cm.
∴两个正六边形的内角都是120°,
每一组对应边的比都是$\frac{3}{4}$,
∴两个正六边形相似;
(2)如图1,过点B,C分别作BM⊥AD,CN⊥AD于点M,N两点,
∵AB=3,∠ABM=30°,
∴AM=$\frac{3}{2}$,
同理DN=$\frac{3}{2}$,
MN=BC=3,
∴AD=6,
如图2,过点B′,C′分别作B′M′⊥A′D′,C′N′⊥A′D′于点M′,N′两点,
∵A′B′=4,∠A′B′M′=30°,
∴A′M′=2,
同理D′N′=2,
M′N′=B′C′=4,
∴A′D′=8,
∴AB:A′B′=3:4.
点评 本题考查了相似多边形的判定和性质,熟练掌握相似多边形的判定和性质是解题的关键.

练习册系列答案
相关题目
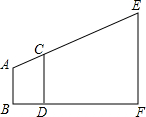 如图,利用标杆测量楼高,已知AB=180m,标杆CD=240m,BD=30m,DF=420m,则楼高EF=1080m.
如图,利用标杆测量楼高,已知AB=180m,标杆CD=240m,BD=30m,DF=420m,则楼高EF=1080m.