题目内容
14.从-1,0,1,2这四个数字中,随机抽取一个数,记为a.那么使关于x的一次函数y1=3x,y2=-3x+a的图象与x轴围成的三角形面积为$\frac{1}{12}$,且使关于x的一元二次方程(a+1)x2+2x+$\frac{1}{2}$=0有两个实数根的概率为$\frac{1}{4}$.分析 首先确定使关于x的一次函数y1=3x,y2=-3x+a的图象与x轴围成的三角形面积为$\frac{1}{12}$的a的值,然后确定使关于x的一元二次方程(a+1)x2+2x+$\frac{1}{2}$=0有两个实数根的a的值,然后利用概率公式求解即可.
解答 解:∵一次函数y1=3x与y2=-3x+a的图象交于($\frac{a}{6}$,$\frac{a}{2}$),
∴一次函数y1=3x,y2=-3x+a的图象与x轴围成的三角形面积为$\frac{1}{2}$×$\frac{|a|}{3}$×$\frac{|a|}{2}$=$\frac{1}{12}$,
解得:a=1或-1,
∵关于x的一元二次方程(a+1)x2+2x+$\frac{1}{2}$=0有两个实数根,
∴22-4×$\frac{1}{2}$(a+1)≥0,
解得:a≤$\frac{1}{2}$,
∴满足条件的只有-1,
∴P=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
4.设一元二次方程x2-2x-4=0的两个实根为x1和x2,则下列结论正确的是( )
| A. | x1+x2=-4 | B. | x1+2=4 | C. | x1+x2=2 | D. | x1+2=-2 |
5.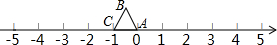 等边△ABC在数轴上的位置如图所示,点A、C对应的数分别为0和-1,若△ABC绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1;则翻转2012次后,点B所对应的数是( )
等边△ABC在数轴上的位置如图所示,点A、C对应的数分别为0和-1,若△ABC绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1;则翻转2012次后,点B所对应的数是( )
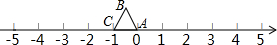 等边△ABC在数轴上的位置如图所示,点A、C对应的数分别为0和-1,若△ABC绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1;则翻转2012次后,点B所对应的数是( )
等边△ABC在数轴上的位置如图所示,点A、C对应的数分别为0和-1,若△ABC绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1;则翻转2012次后,点B所对应的数是( )| A. | 2013 | B. | 2010 | C. | 2011 | D. | 2012 |
9.使$\sqrt{a-1}$有意义的a的取值范围是( )
| A. | a>1 | B. | a≤1 | C. | a<1 | D. | a≥1 |
19.下列方程:$xy+1=1,\sqrt{{x^2}-1}=2,\frac{1}{t}+{t^2}=1$,x(x+1)=x(x-2)+5,ax2+bx+cx2=0,x2-y+1=0,其中是一元二次方程的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
6.已知线段a=l,c=5,线段b是线段a、c的比例中项,线段b的值为( )
| A. | 2.5 | B. | $\sqrt{5}$ | C. | ±2.5 | D. | ±$\sqrt{5}$ |