题目内容
10. 观察下列各个等式:12=1,12+22=5,12+22+32=14,12+22+32+42=30,….
观察下列各个等式:12=1,12+22=5,12+22+32=14,12+22+32+42=30,….(1)你能从中推导出计算12+22+32+42+…+n2的公式吗?请写出你的推导过程;
(2)请你用(1)中推导出的公式来解决下列问题:
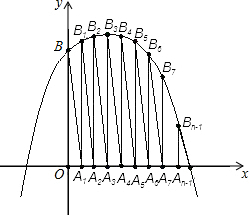
已知:如图,抛物线y=-x2+2x+3与x、y轴的正半轴分别交于点A、B,将线段OAn等分,分点从左到右依次为A1、A2、A3、A4、A5、A6、…、An-1,分别过这n-1个点作x轴的垂线依次交抛物线于点B1、B2、B3、B4、B5、B6、…、Bn-1,设△OBA1、△A1B1A2、△A2B2A3、△A3B3A4、…、△An-1Bn-1A的面积依次为S1、S2、S3、S4、…、Sn.
①当n=2013时,求s1+s2+s3+s4+…+s2013的值;
②试探究:当n取到无穷无尽时,题中所有三角形的面积和将是什么值?为什么?
分析 (1)由n3-(n-1)3=3n2-3n+1公式的n的式子相加推导出12+22+32+42+…+n2的公式.
(2)①结合抛物线和(1)中推导出的公式求出S1+S2+S3+S4+S5+…+S2013的值;
②当n取到无穷无尽时,取极值,求得三角形的面积.
解答 解:(1)∵n3-(n-1)3=3n2-3n+1,∴当式中的n从1、2、3、…依次取到n时,就可得下列n个等式:
13-03=3×12-3×1+1,23-13=3×22-3×2+1,33-23=3×32-3×3+1…n3-(n-1)3=3n2-3n+1,
将这n个等式的左右两边分别相加得:n3=3(12+22+32+…n2)-3(1+2+3+…+n)+n,
即12+22+32+…n2=$\frac{{n}^{3}+3(1+2+3+…n)-n}{3}$=$\frac{n(n+1)(2n+1)}{6}$.
(2)先求得A、B两点的坐标分别为(3,0),(0,3),∴点A1($\frac{3}{n}$,0)A2($\frac{6}{n}$,0)A3($\frac{9}{n}$,0)A4($\frac{12}{4}$,0)…An-1($\frac{3(n-1)}{n}$,0),
点B1($\frac{3}{n}$,-($\frac{3}{n}$)2+2($\frac{3}{n}$)+3),B2($\frac{6}{n}$,-($\frac{6}{n}$)2+2($\frac{6}{n}$)+3)…Bn-1($\frac{3(n-1)}{n}$,-[$\frac{3(n-1)}{n}$]2+2$\frac{3(n-1)}{n}$+3),
∴S1=$\frac{9}{2n}$,S2=$\frac{9({n}^{2}+2n-3)}{2{n}^{3}}$,S3=$\frac{9({n}^{2}+4n-12)}{2{n}^{3}}$…Sn=$\frac{9[{n}^{2}+2({n}^{2}-n)-3(n-1)^{2}]}{2{n}^{3}}$
∴S1+S2+S3+…+Sn=$\frac{9\{{n}^{3}+2n(1+2+…+n-1)-3[{1}^{2}+{2}^{2}+…+(n-1)^{2}]\}}{2{n}^{3}}$
=$\frac{9[{n}^{3}+2n×\frac{n(n-1)}{2}-3×\frac{n(n+1)(2n-1)}{6}]}{2{n}^{3}}$=$\frac{9(2{n}^{2}+n-1)}{4{n}^{2}}$.
∴①当n=2013时,S1+S2+S3+S4+…S2013=$\frac{9(2×201{3}^{2}+2012)}{4×201{3}^{2}}$;
②∵S1+S2+S3+…Sn=$\frac{9(2{n}^{2}+n-1)}{4{n}^{2}}$=$\frac{9}{2}$+$\frac{9}{4n}$-$\frac{9}{4{n}^{2}}$,
∴当n取到无穷无尽时,上式的值等于$\frac{9}{2}$,即所有三角形的面积和等于$\frac{9}{2}$.
点评 本题考查了二次函数综合题,(1)利用立方差公式推导是解题关键,(2)利用等分得出A点坐标,利用点在函数图象上得出B点坐标,利用推导公式求出面积的和,计算是解题关键.

 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案| A. | 6 | B. | -6 | C. | 1 | D. | 0 |
| A. | m≤3 | B. | m<3 | C. | m<3且m≠2 | D. | m≤3且m≠2 |
| A. | 2sinαcosα | B. | sinα | C. | cosα | D. | cos2α |
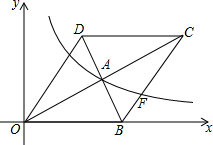 如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是(12,$\frac{8}{3}$).
如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是(12,$\frac{8}{3}$).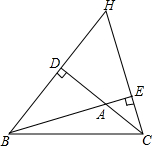 已知BD、CE是△ABC的两条高,直线BD、CE相交于点H.
已知BD、CE是△ABC的两条高,直线BD、CE相交于点H.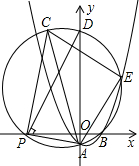 如图,在平面直角坐标系中,抛物线y═$\frac{1}{2}$x2+bx+c经过点A(0,-1),B(2,0)P(t,0)是x轴负半轴上一动点,过点P作PA的垂线交△PAB的外接圆于点C,△PAB的外接圆与y轴交于点D,与抛物线在第一象限限交于点E.
如图,在平面直角坐标系中,抛物线y═$\frac{1}{2}$x2+bx+c经过点A(0,-1),B(2,0)P(t,0)是x轴负半轴上一动点,过点P作PA的垂线交△PAB的外接圆于点C,△PAB的外接圆与y轴交于点D,与抛物线在第一象限限交于点E.