题目内容
6.计算:($\frac{2}{{a}^{2}-{b}^{2}}$-$\frac{1}{{a}^{2}-ab}$)÷$\frac{a}{a+b}$.分析 首先将括号里面通分运算,进而利用分式的性质化简求出即可.
解答 解:($\frac{2}{{a}^{2}-{b}^{2}}$-$\frac{1}{{a}^{2}-ab}$)÷$\frac{a}{a+b}$
=[$\frac{2}{(a+b)(a-b)}$-$\frac{1}{a(a-b)}$]×$\frac{a+b}{a}$
=[$\frac{2a}{a(a+b)(a-b)}$-$\frac{a+b}{a(a+b)(a-b)}$]×$\frac{a+b}{a}$
=$\frac{2a-(a+b)}{a(a+b)(a-b)}$×$\frac{a+b}{a}$
=$\frac{1}{{a}^{2}}$.
点评 此题主要考查了分式的混合运算,正确进行通分运算是解题关键.

练习册系列答案
相关题目
14. 如图,正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )
如图,正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )
 如图,正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )
如图,正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )| A. | x<-2或x>2 | B. | x<-2或0<x<2 | C. | -2<x<0或0<x<2 | D. | -2<x<0或x>2 |
18.计算3+(-3)的结果是( )
| A. | 6 | B. | -6 | C. | 1 | D. | 0 |
15.关于x的一元二次方程(m-2)x2+2x+1=0有实数根,则m的取值范围是( )
| A. | m≤3 | B. | m<3 | C. | m<3且m≠2 | D. | m≤3且m≠2 |
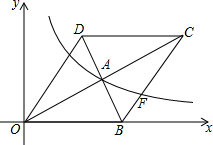 如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是(12,$\frac{8}{3}$).
如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是(12,$\frac{8}{3}$).