题目内容
2.理解与思考:在某次作业中有这样的一道题:“如果代数式5a+3b的值为-4,那么代数式2(a+b)+4(2a+b)的值是多少?”小明是这样来解的:
原式=2a+2b+8a+4b=10a+6b
把式子5a+3b=-4两边同乘以2,得10a+6b=-8.
仿照小明的解题方法,完成下面的问题:
(1)如果a2+a=0,则a2+a+2015=2015.
(2)已知a-b=-3,求3(a-b)-5a+5b+5的值.
(3)已知a2+2ab=-2,ab-b2=-4,求2a2+$\frac{7}{2}$ab+$\frac{1}{2}$b2的值.
分析 (1)把已知等式代入原式计算即可得到结果;
(2)原式变形后,两已知等式代入计算即可求出值;
(3)原式变形后,将已知等式代入计算即可求出值.
解答 解:(1)∵a2+a=0,
∴原式=2015;
故答案为:2015;
(2)原式=3a-3b-5a+5b+5=-2(a-b)+5,
当a-b=-3时,原式=6+5=11;
(3)原式=$\frac{1}{2}$(4a2+7ab+b2)=$\frac{1}{2}$[4(a2+2ab)-(ab-b2)],
当a2+2ab=-2,ab-b2=-4时,原式=$\frac{1}{2}$×(-8+4)=-2.
点评 此题考查了整式的加减-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
12.某品牌电脑销售公司有营销员14人,销售部为制定营销人员月销售电脑定额,统计了这14人某月的销售量如下(单位:台):
(1)求这14位营销员该月销售该品牌电脑的平均数、中位数和众数.
(2)销售部经理把每位营销员月销售量定为90台,你认为是否合理?为什么?
| 销售量 | 200 | 170 | 130 | 80 | 50 | 40 |
| 人 数 | 1 | 1 | 2 | 5 | 3 | 2 |
(2)销售部经理把每位营销员月销售量定为90台,你认为是否合理?为什么?
10.若x2+ax-2y+7-(bx2-2x+9y-1)的值与x的无关,则-a-b的值为( )
| A. | 3 | B. | 1 | C. | -2 | D. | 2 |
7.下列方程是一元二次方程的是( )
| A. | ax2-2x+=0(a是已知数) | B. | 3x2+2x-4=3x2 | ||
| C. | 5x2-2x=0 | D. | $\frac{{x}^{3}+2x}{x}$=1 |
 如图,在数轴上点A、B所表示的数分别为m,n,则m+n符号为正或者“+”.
如图,在数轴上点A、B所表示的数分别为m,n,则m+n符号为正或者“+”.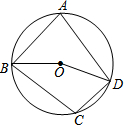 如图,四边形ABCD内接于⊙O,若∠BOD=160°,则∠BCD=100°.
如图,四边形ABCD内接于⊙O,若∠BOD=160°,则∠BCD=100°. 如图,反比例函数y=$\frac{18}{x}$的图象过矩形OABC的顶点B,OA、OC分别在x轴、y轴的正半轴上,OA;OC=1:2,矩形OABC的对角线交于点E.
如图,反比例函数y=$\frac{18}{x}$的图象过矩形OABC的顶点B,OA、OC分别在x轴、y轴的正半轴上,OA;OC=1:2,矩形OABC的对角线交于点E.