题目内容
8.(1)填空:$\root{3}{{a}^{3}}$=a,$\root{3}{{a}^{6}}$=a2,$\root{3}{{a}^{9}}$=a3;(2)根据(1)的计算,你有什么发现?请说明理由.
分析 (1)原式各项计算得到结果;
(2)根据(1)的结果得出一般性结论,验证即可.
解答 解:(1)$\root{3}{{a}^{3}}$=a,$\root{3}{{a}^{6}}$=a2,$\root{3}{{a}^{9}}$=a3;
(2)发现:$\root{3}{{a}^{3n}}$=an,
∵a3n=(an)3,
∴$\root{3}{{a}^{3n}}$=an.
点评 此题考查了立方根,熟练掌握立方根的定义是解本题的关键.

练习册系列答案
相关题目
19.如果一个三角形两边的长分别等于一元二次方程x2-17x+66=0的两个实数根,那么这个三角形的周长可能是( )
| A. | 22 | B. | 23 | C. | 35 | D. | 36 |
16.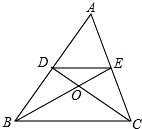 如图已知:△ABC中,DE∥BC,BE,CD交于点O,S△DOE:S△BOC=4:25,则AD:DB=( )
如图已知:△ABC中,DE∥BC,BE,CD交于点O,S△DOE:S△BOC=4:25,则AD:DB=( )
 如图已知:△ABC中,DE∥BC,BE,CD交于点O,S△DOE:S△BOC=4:25,则AD:DB=( )
如图已知:△ABC中,DE∥BC,BE,CD交于点O,S△DOE:S△BOC=4:25,则AD:DB=( )| A. | 2:5 | B. | 2:3 | C. | 4:9 | D. | 3:5 |
20.(-$\frac{1}{4}$)2006×(-4)2007的结果是( )
| A. | -1 | B. | 1 | C. | -$\frac{1}{4}$ | D. | -4 |
4.多项式72x2-x是( )
| A. | 一次二项式 | B. | 二次二项式 | C. | 四次二项式 | D. | 五次二项式 |
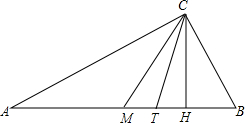 在△ABC中,M是AB中点,CH⊥AB于H,CT是∠ACB和∠MCH的平分线.求证:△ABC是直角三角形.
在△ABC中,M是AB中点,CH⊥AB于H,CT是∠ACB和∠MCH的平分线.求证:△ABC是直角三角形.