题目内容
16．
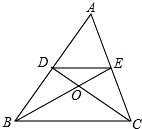如图已知：△ABC中，DE∥BC，BE，CD交于点O，S△DOE：S△BOC=4：25，则AD：DB=（ ）| A． | 2：5 | B． | 2：3 | C． | 4：9 | D． | 3：5 |
分析 由DE∥BC，得到△DOE∽△BOC，根据相似三角形的性质即可得到结论．
解答 解：∵DE∥BC，
∴△DOE∽△BOC，
∴S△DOE：S△BOC=DE2：BC2=4：25，
∴$\frac{AD}{AB}=\frac{DE}{BC}$=$\frac{2}{5}$．
∴AD：DB=2：3，
故选B．
点评 本题考查了相似三角形的判定，考查了相似三角形对应边比例相等的性质，熟练掌握相似三角形的判定和性质是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
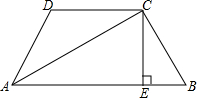如图，四边形ABCD中，CE⊥AB于E，将①AC平分∠BAD；②CB=CD；③∠B+∠ADC=180°；④AB+AD=2AE中的任意两个作为条件，都可得出另两个结论，请你一一探究，并任选一种情形予以证明．
抛物线y=ax2+bx+c的图象如图所示，则当y≤3时，求x的取值范围．