题目内容
19．如果一个三角形两边的长分别等于一元二次方程x2-17x+66=0的两个实数根，那么这个三角形的周长可能是（ ）| A． | 22 | B． | 23 | C． | 35 | D． | 36 |
分析 先利用因式分解法解方程得到x1=6，x2=11，即三角形两边为6和11，再利用三角形三边的关系得到第三边的范围，从而可得三角形周长的范围，于是可对四个选项进行判断．
解答 解：x2-17x+66=0
（x-6）（x-11）=0，
x-6=0或x-11=0，
所以x1=6，x2=11，
即三角形两边为6和11，
所以三角形第三边x的范围为5＜x＜17，
所以这个三角形的周长l的范围为22＜l＜34．
故选B．
点评 本题考查了解一元二次方程-因式分解法：先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．也考查了三角形三边的关系．
练习册系列答案
阅读快车系列答案
相关题目
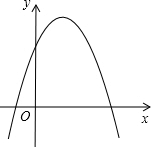二次函数y=ax2+bx+c（a≠0）的图象如图所示，则：a＜0；b＞0；c＞0；b2-4ac＞0．
抛物线y=ax2+bx+c的图象如图所示，则当y≤3时，求x的取值范围．