题目内容
14.计算或化简:(1)$\frac{2}{{\sqrt{2}}}$+(-$\sqrt{2}$+1)0-2sin45°
(2)$\frac{{{x^2}-1}}{{{x^2}+x}}÷({x-\frac{2x-1}{x}})$.
分析 (1)根据二次根式的化简、零指数幂以及特殊角的三角函数进行计算即可;
(2)根据运算顺序,先算括号里面的,再算除法即可.
解答 解:(1)$\frac{2}{{\sqrt{2}}}$+(-$\sqrt{2}+1$)0-2sin45°
=$\sqrt{2}$+1-2×$\frac{\sqrt{2}}{2}$
=$\sqrt{2}$+1-$\sqrt{2}$
=1;
(2)原式═$\frac{x-1}{x}÷\frac{{{{(x-1)}^2}}}{x}$
=$\frac{x-1}{x}$•$\frac{x}{(x-1)^{2}}$
=$\frac{1}{x-1}$.
点评 本题考查了二次根式的混合运算以及分式的化简,分式的约分和通分是解题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
4.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)间有下面的关系:
下列说法不正确的是( )
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 10 | 10.5 | 11 | 11.5 | 12 | 12.5 |
| A. | x与y都是变量,且x是自变量,y是因变量 | |
| B. | 所挂物体质量为4kg时,弹簧长度为12cm | |
| C. | 弹簧不挂重物时的长度为0cm | |
| D. | 物体质量每增加1kg,弹簧长度y增加0.5cm |
5.如果8排6座记作(8,6),那么(3,5)表示( )
| A. | 3排5座 | B. | 5排3座 | C. | 5排5座 | D. | 3排3座 |
2.已知圆锥的底面半径为4cm,高为3cm,则圆锥的侧面积是( )
| A. | 20cm2 | B. | 20πcm2 | C. | 12πcm2 | D. | 10πcm2 |
19.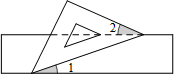 如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上,则∠1+∠2=( )
如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上,则∠1+∠2=( )
 如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上,则∠1+∠2=( )
如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上,则∠1+∠2=( )| A. | 30° | B. | 45° | C. | 25° | D. | 15° |
6.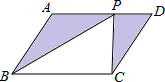 如图,P是?ABCD上一点.已知S△ABP=3,S△PDC=2,那么平行四边形ABCD的面积是( )
如图,P是?ABCD上一点.已知S△ABP=3,S△PDC=2,那么平行四边形ABCD的面积是( )
 如图,P是?ABCD上一点.已知S△ABP=3,S△PDC=2,那么平行四边形ABCD的面积是( )
如图,P是?ABCD上一点.已知S△ABP=3,S△PDC=2,那么平行四边形ABCD的面积是( )| A. | 6 | B. | 8 | C. | 10 | D. | 无法确定 |
 如图,点A、B在直线l上,AB=10cm,⊙B的半径为1cm,点C在直线l上,过点C作直线CD且∠DCB=30°,直线CD从A点出发以每秒4cm的速度自左向右平行运动,与此同时,⊙B的半径也不断增大,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0),当直线CD出发$\frac{4}{3}$或6秒直线CD恰好与⊙B相切.
如图,点A、B在直线l上,AB=10cm,⊙B的半径为1cm,点C在直线l上,过点C作直线CD且∠DCB=30°,直线CD从A点出发以每秒4cm的速度自左向右平行运动,与此同时,⊙B的半径也不断增大,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0),当直线CD出发$\frac{4}{3}$或6秒直线CD恰好与⊙B相切.