题目内容
3.如图,已知∠ABC=90°,△ABD是等边三角形,点P为射线BC上任意一点(点P与点B不重合),连结AP,作∠PAE=60°,使AE=AP.连结ED并延长交射线BC于点F.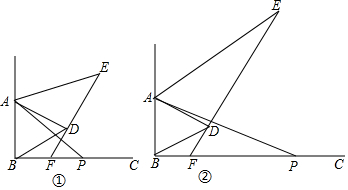
(1)如图①,当点P运动到使AP在∠BAD内部时,求∠ADE与∠EFC的度数;
(2)如图②,当点P运动到使AP在∠BAD外部时,图中∠ADE与∠EFC的度数发生变化吗?试说明理由.
分析 (1)只要证明△PAB≌△EAD,可得∠ADE=∠ABP,由∠ABC=90°,推出∠ADE=90°,在四边形ABFD中,∠BFD=360°-∠BAD-∠ABF-∠ADF=120°,由此即可求出∠EFC.
(2)∠ADE与∠EFC的度数不发生变化.证明方法类似(1).
解答 解:(1)如图①中,
∵△ABD是等边三角形,
∴AB=AD,∠BAD=∠EAP=60°,
∴∠PAB=∠EAD,
在△PAB和△EAD中,
$\left\{\begin{array}{l}{PA=AE}\\{∠PAB=∠EAD}\\{AB=AD}\end{array}\right.$,
∴△PAB≌△EAD,
∴∠ADE=∠ABP,
∵∠ABC=90°,
∴∠ADE=90°,
在四边形ABFD中,∠BFD=360°-∠BAD-∠ABF-∠ADF=120°,
∴∠EFC=180°-∠BFD=60°.
(2)如图②中,∠ADE与∠EFC的度数不发生变化,理由如下,
∵△ABD是等边三角形,
∴AB=AD,∠BAD=∠EAP=60°,
∴∠PAB=∠EAD,
在△PAB和△EAD中,
$\left\{\begin{array}{l}{PA=AE}\\{∠PAB=∠EAD}\\{AB=AD}\end{array}\right.$,
∴△PAB≌△EAD,
∴∠ADE=∠ABP,
∵∠ABC=90°,
∴∠ADE=90°,
在四边形ABFD中,∠BFD=360°-∠BAD-∠ABF-∠ADF=120°,
∴∠EFC=180°-∠BFD=60°.
点评 本题考查全等三角形的判定和性质、等边三角形的性质、四边形内角和定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
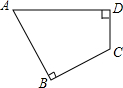 如图,在四边形ABCD中,∠B=∠D=90°,∠A=60°,BC=2,CD=1,求AD的长.
如图,在四边形ABCD中,∠B=∠D=90°,∠A=60°,BC=2,CD=1,求AD的长.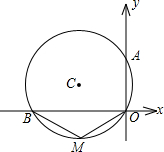 如图,⊙C过原点,且与两坐标轴分别交于点A、B,点A的坐标为(0,2),M为第三象限内弧$\widehat{OB}$上一点,∠BMO=120°,则⊙C的半径为2.
如图,⊙C过原点,且与两坐标轴分别交于点A、B,点A的坐标为(0,2),M为第三象限内弧$\widehat{OB}$上一点,∠BMO=120°,则⊙C的半径为2.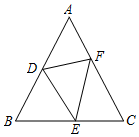 如图,△ABC中,∠B=∠C,D、E、F分别在AB、BC、AC上,且∠B=∠DEF,BD=CE,求证:ED=EF.
如图,△ABC中,∠B=∠C,D、E、F分别在AB、BC、AC上,且∠B=∠DEF,BD=CE,求证:ED=EF. 如图,点M在等边三角形ABC的BC边上,延长BA至N,使AN=MC,连接MN交AC于点O,求证:OM=ON.
如图,点M在等边三角形ABC的BC边上,延长BA至N,使AN=MC,连接MN交AC于点O,求证:OM=ON.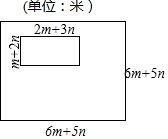 如图,某体育训练基地,有一块边长为(6m+5n)米的正方形土地,现准备在这块正方形土地上修建一个长为(2m+3n)米,宽为(m+2n)米的长方形游泳池,剩余部分则全部修建成休息区域.(结果化简)
如图,某体育训练基地,有一块边长为(6m+5n)米的正方形土地,现准备在这块正方形土地上修建一个长为(2m+3n)米,宽为(m+2n)米的长方形游泳池,剩余部分则全部修建成休息区域.(结果化简) 如图,△ABC中,AD是△ABC的边BC上的高,E、F分别是AB、AC的中点,AC=13、AB=20、BC=21.
如图,△ABC中,AD是△ABC的边BC上的高,E、F分别是AB、AC的中点,AC=13、AB=20、BC=21.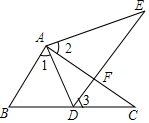 如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE.求证:
如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE.求证: