题目内容
11.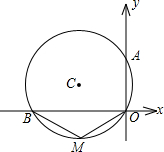 如图,⊙C过原点,且与两坐标轴分别交于点A、B,点A的坐标为(0,2),M为第三象限内弧$\widehat{OB}$上一点,∠BMO=120°,则⊙C的半径为2.
如图,⊙C过原点,且与两坐标轴分别交于点A、B,点A的坐标为(0,2),M为第三象限内弧$\widehat{OB}$上一点,∠BMO=120°,则⊙C的半径为2.
分析 连接AB,由条件可知AB为圆的直径,再根据圆内接四边形的性质可求得∠BAO,再利用直角三角形的性质可求得AB,则可求得圆的半径.
解答  解:
解:
连接AB,
∵∠AOB=90°,
∴AB为⊙C的直径,
∵∠BMO=120°,
∴∠BAO=60°,
∴∠ABO=30°,
∴AB=2AO=4,
∴⊙C的半径为2,
故答案为:2.
点评 本题主要考查圆周角定理和圆内接四边形的性质,求得AB为直径,进一步求得∠BAO是解题的关键.

练习册系列答案
相关题目
15.下列命题的逆命题是真命题的是( )
| A. | 对顶角相等 | B. | 两直线平行,内错角相等 | ||
| C. | 全等三角形的对应角相等 | D. | 第一象限内点的横坐标是正数 |
2.要使a5<a3<a<a2<a4成立,则a的取值范围是( )
| A. | 0<a<1 | B. | a>1 | C. | -1<a<0 | D. | a<-1 |
20.关于x的方程4x+a-5=0与3x-9=0的解相同,那么a的值为( )
| A. | 17 | B. | -17 | C. | 7 | D. | -7 |
 如图,在△ABC中,AB=AC,BC=12,BD为高,M为AB中点,且DM=5,则△ABC的面积为48.
如图,在△ABC中,AB=AC,BC=12,BD为高,M为AB中点,且DM=5,则△ABC的面积为48.