题目内容
9.若抛物线y=x2+bx+c与x轴、y轴交于三个不同的点A、B、C,当实数b、c变化时,△ABC的外接圆一定经过定点,此定点的坐标为(0,1).分析 先设出A、B、C三点的坐标,三角形外接圆的圆心是三边垂直平分线的交点,再根据圆上各点到圆心的距离相等,最终通过讨论可以得到不管b、c如何变换,外接圆都过一个定点,从而解答此题.
解答 解:设抛物线与x轴的交点A的坐标为(x1,0),B的坐标为(x2,0),与y轴交点C的坐标为(0,c)
∵x1+x2=-b,x1x2=c
三角形外接圆的圆心在边AB的垂直的平分线上,即在在抛物线的对称轴$x=-\frac{b}{2}$上,故设圆心P的坐标为$(-\frac{b}{2},t)$
PA2=PC2
∴$({x}_{1}+\frac{b}{2})^{2}+{t}^{2}=(-\frac{b}{2})^{2}+(t-c)^{2}$
展开化简,得
${{x}_{1}}^{2}+b{x}_{1}={c}^{2}-2tc$
得$t=\frac{{{x}_{1}}^{2}+b{x}_{1}-{c}^{2}}{-2c}$
∵${{x}_{1}}^{2}+b{x}_{1}+c=0$
∴$t=\frac{-c-{c}^{2}}{-2c}$
得t=$\frac{c+1}{2}$,$t-c=\frac{1-c}{2}$
∴圆的半径得平方=PC2=$\frac{{b}^{2}}{4}+(\frac{1-c}{2})^{2}$
∴圆的方程为:$(x+\frac{b}{2})^{2}+(y-\frac{c+1}{2})^{2}=(\frac{b}{4})^{2}+(\frac{1-c}{2})^{2}$
故当x=0时,y=1,所以不管b、c怎么变化,点(0,1)都满足圆的方程
故答案为:(0,1)
点评 本题考察抛物线与圆的关系,其中需要知道两点间的距离公式,三角形的外接圆圆心是三角形三边的垂直平分线交点.

练习册系列答案
相关题目
4.若记y=f(x)=$\frac{x}{1+x}$,其中f(1)表示当x=1时y的值,即f(1)=$\frac{1}{1+1}$=$\frac{1}{2}$,f($\frac{1}{2}$)表示当x=$\frac{1}{2}$时y的值,即f($\frac{1}{2}$)=$\frac{\frac{1}{2}}{1+\frac{1}{2}}$=$\frac{1}{3}$,则f(1)+f(2)+f($\frac{1}{2}$)+f(3)+f($\frac{1}{3}$)+…+f(99)+f($\frac{1}{99}$)=( )
| A. | 99$\frac{1}{2}$ | B. | 98$\frac{1}{2}$ | C. | 99 | D. | 98 |
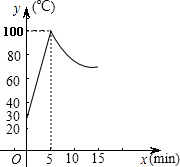 要制作一种糖制工艺品,需先把材料加热到40℃~100℃才能进行操作.设材料温度为y(℃),从加热开始计算的时间为x(min).经实验,该材料加热时,温度y与时间x的函数关系图象是一条线段;停止加热后,温度y与时间x的函数关系图象的一部分.已知该材料加热前的温度是30℃,加热5min时温度达到100℃
要制作一种糖制工艺品,需先把材料加热到40℃~100℃才能进行操作.设材料温度为y(℃),从加热开始计算的时间为x(min).经实验,该材料加热时,温度y与时间x的函数关系图象是一条线段;停止加热后,温度y与时间x的函数关系图象的一部分.已知该材料加热前的温度是30℃,加热5min时温度达到100℃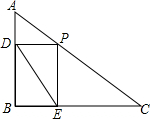 如图,在△ABC中,∠B=90°,AB=15cm,∠A=60°,动点P从点A开始沿AC边向C以2cm/s的速度移动(不与C重合),过P作PD∥BC交AB于D,过P作PE∥AB交BC于E,连接DE,若P点运动的时间为ts.
如图,在△ABC中,∠B=90°,AB=15cm,∠A=60°,动点P从点A开始沿AC边向C以2cm/s的速度移动(不与C重合),过P作PD∥BC交AB于D,过P作PE∥AB交BC于E,连接DE,若P点运动的时间为ts.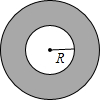 如图,大圆的半径是R.
如图,大圆的半径是R.