题目内容
14.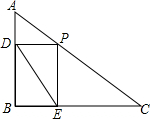 如图,在△ABC中,∠B=90°,AB=15cm,∠A=60°,动点P从点A开始沿AC边向C以2cm/s的速度移动(不与C重合),过P作PD∥BC交AB于D,过P作PE∥AB交BC于E,连接DE,若P点运动的时间为ts.
如图,在△ABC中,∠B=90°,AB=15cm,∠A=60°,动点P从点A开始沿AC边向C以2cm/s的速度移动(不与C重合),过P作PD∥BC交AB于D,过P作PE∥AB交BC于E,连接DE,若P点运动的时间为ts.(1)设四边形ADEC的面积为ycm2,求y与t之间的函数关系式,并写出自变量t的取值范围;
(2)当t为何值时,DE的长取最小值?并求出这个最小值.
分析 (1)解直角三角形得到∠C=30°,AC=2AB=30,BC=15$\sqrt{3}$,由PD∥BC,得到∠APD=∠C=30°,求得AD=t,PD=$\sqrt{3}$t,于是得BE=PD=$\sqrt{3}$t,BD=15-t,于是求得结论;
(2)根据勾股定理得到DE=$\sqrt{(\sqrt{3}t)^{2}+(15-t)^{2}}$=$\sqrt{4{t}^{2}-30t+225}$=$\sqrt{4(t-\frac{15}{4})^{2}+\frac{675}{4}}$,于是求得当t=$\frac{15}{4}$s时,DE有最小值,DE的最小值为$\frac{15\sqrt{3}}{2}$.
解答  解:(1)∵∠B=90°,AB=15cm,∠A=60°,
解:(1)∵∠B=90°,AB=15cm,∠A=60°,
∴∠C=30°,
∴AC=2AB=30,BC=15$\sqrt{3}$,
由题意得:AP=2t,
∵PD∥BC,
∴∠APD=∠C=30°,
∴AD=t,PD=$\sqrt{3}$t,
∴BE=PD=$\sqrt{3}$t,BD=15-t,
∴y=S△ABC-S△BDE=$\frac{1}{2}$×15$\sqrt{3}$×15-$\frac{1}{2}$(15-t)•$\sqrt{3}$t,
即:y=$\frac{\sqrt{3}}{2}$t2-$\frac{15\sqrt{3}}{2}$t+$\frac{225\sqrt{3}}{2}$(0<t<15);
(2)∵BE2+BD2=DE2,
∴DE=$\sqrt{(\sqrt{3}t)^{2}+(15-t)^{2}}$=$\sqrt{4{t}^{2}-30t+225}$=$\sqrt{4(t-\frac{15}{4})^{2}+\frac{675}{4}}$,
∴当t=$\frac{15}{4}$s时,DE有最小值,DE的最小值为$\frac{15\sqrt{3}}{2}$.
点评 本题考查了勾股定理,解直角三角形,三角形的面积,二次函数的最值,根据四边形ADEC的面积=S△ABC-S△BDE求出y与t之间的函数关系式是解题的关键.

| A. | -2 | B. | 2 | C. | $\frac{10}{3}$ | D. | -$\frac{10}{3}$ |
| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
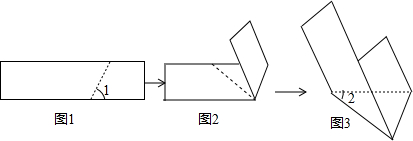
 如图,将一个直角三角形模型的直角顶点放在直尺的一边上,若∠1=55°,∠2=60°,则∠3=25°.
如图,将一个直角三角形模型的直角顶点放在直尺的一边上,若∠1=55°,∠2=60°,则∠3=25°.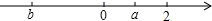 看数轴,化简:|a|-|b|+|a-2|.
看数轴,化简:|a|-|b|+|a-2|.