题目内容
4．已知25x=2000，80y=2000，求x+y-xy的值．分析 因x、y为指数，我们目前无法求出x、y的值，$\frac{1}{x}$+$\frac{1}{y}$=$\frac{x+y}{xy}$，其实只需求出x+y、xy的值或它们的关系，自然想到指数运算律．
解答 解：由已知得2000${\;}^{\frac{1}{x}}$=25，2000${\;}^{\frac{1}{y}}$=80，
两式相乘，得2000${\;}^{\frac{1}{x}}$$\frac{×}{\;}$2000${\;}^{\frac{1}{y}}$=25×80=2000，
故$\frac{1}{x}$+$\frac{1}{y}$=$\frac{x+y}{xy}$=1，
∴x+y=xy，
∴x+y-xy=0．
点评 本题考查了同底数幂的乘法运算法则，将已知条件转化为分数指数是解题的关键．
练习册系列答案
相关题目
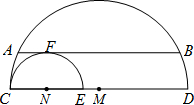如图，CD为大半圆M的直径，E为CM上一点，以CE为直径画小半圆N，大半圆M的弦AB与小半圆N相切于点F，且AB∥CD，AB=4，设$\widehat{CD}$、$\widehat{CE}$的长分别为x、y，线段ED的长为z，则z（x+y）的值为8π．
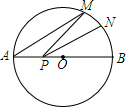如图，AB是⊙O的直径，AB=10，点M在⊙O上，∠MAB=30°，N是弧MB的中点，P是直径AB上的一动点，若MN=2，则△PMN周长的最小值为5$\sqrt{2}$+2．
16．如图所示，（1）1张餐桌可坐6人，2张餐桌可坐10人；
（2）按照图中的方式继续排列餐桌，完成下表：
（3）每增加-张桌子，可多坐4人；
（4）摆n张桌子时可坐4n+2人；
（5）一家餐厅有长方形桌子30张，现在有131个客人要吃饭，那该如何摆拼桌子？
（2）按照图中的方式继续排列餐桌，完成下表：
| 桌子张数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 可坐人数 |
（3）每增加-张桌子，可多坐4人；
（4）摆n张桌子时可坐4n+2人；
（5）一家餐厅有长方形桌子30张，现在有131个客人要吃饭，那该如何摆拼桌子？