题目内容
4.若记y=f(x)=$\frac{x}{1+x}$,其中f(1)表示当x=1时y的值,即f(1)=$\frac{1}{1+1}$=$\frac{1}{2}$,f($\frac{1}{2}$)表示当x=$\frac{1}{2}$时y的值,即f($\frac{1}{2}$)=$\frac{\frac{1}{2}}{1+\frac{1}{2}}$=$\frac{1}{3}$,则f(1)+f(2)+f($\frac{1}{2}$)+f(3)+f($\frac{1}{3}$)+…+f(99)+f($\frac{1}{99}$)=( )| A. | 99$\frac{1}{2}$ | B. | 98$\frac{1}{2}$ | C. | 99 | D. | 98 |
分析 根据题意得到f(x)+f($\frac{1}{x}$)=1,原式结合后,计算即可得到结果.
解答 解:∵f(x)=$\frac{x}{1+x}$,f($\frac{1}{x}$)=$\frac{\frac{1}{x}}{1+\frac{1}{x}}$=$\frac{1}{x+1}$,
∴f(x)+f($\frac{1}{x}$)=$\frac{x}{1+x}$+$\frac{1}{x+1}$=$\frac{x+1}{x+1}$=1,
则原式=f(1)+[f(2)+f($\frac{1}{2}$)]+[f(3)+f($\frac{1}{3}$)]+…+[f(99)+f($\frac{1}{99}$)]=$\frac{1}{2}$+1+1+…+1=98$\frac{1}{2}$.
故选B.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.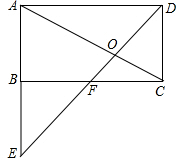 如图所示,矩形ABCD,F为BC中点,DF延长线交直线AB的延长线于E,与AC交于O点,则O点到直线AB和直线CD的距离之比为( )
如图所示,矩形ABCD,F为BC中点,DF延长线交直线AB的延长线于E,与AC交于O点,则O点到直线AB和直线CD的距离之比为( )
 如图所示,矩形ABCD,F为BC中点,DF延长线交直线AB的延长线于E,与AC交于O点,则O点到直线AB和直线CD的距离之比为( )
如图所示,矩形ABCD,F为BC中点,DF延长线交直线AB的延长线于E,与AC交于O点,则O点到直线AB和直线CD的距离之比为( )| A. | 1:2 | B. | 2:1 | C. | 1:3 | D. | 2:3 |
13.某商店出售货物时,要在进价的基础上加一定的利润,下表体现了其数量x(个)与售价y(元)的对应关系,根据表中提供的信息可知y与x之间的关系式是y=8+0.2x.
| 数量x(个) | 1 | 2 | 3 | 4 | 5 |
| 售价y(元) | 8+0.2 | 8+0.4 | 8+0.6 | 8+0.8 | 8+1.0 |
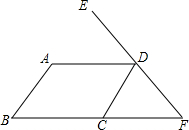 如图,AB∥CD,AD∥BC,∠B=60°,∠EDA=50°,求∠CDF.
如图,AB∥CD,AD∥BC,∠B=60°,∠EDA=50°,求∠CDF. 如图,a,b是两条交叉的公路,为了能够节省成本,包括车辆的机械损耗、省油、省时间等等,市路政管理部门决定在公路a的A处修一条与公路b平行的高速公路c,同时在高速公路c上建一个加油站B,要求该加油站到a,b两条公路的距离相等,请用尺规作图画出公路c以及加油站B的位置(不写已知,求作和作法,保留作图痕迹)
如图,a,b是两条交叉的公路,为了能够节省成本,包括车辆的机械损耗、省油、省时间等等,市路政管理部门决定在公路a的A处修一条与公路b平行的高速公路c,同时在高速公路c上建一个加油站B,要求该加油站到a,b两条公路的距离相等,请用尺规作图画出公路c以及加油站B的位置(不写已知,求作和作法,保留作图痕迹)