题目内容
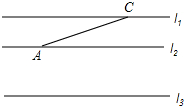 如图,已知直线l1∥l2∥l3,且l1,l2之间的距离为1,l2,l3之间的距离为2,点A、C分别在直线l2,l1上,
如图,已知直线l1∥l2∥l3,且l1,l2之间的距离为1,l2,l3之间的距离为2,点A、C分别在直线l2,l1上,(1)利用直尺和圆规作出以AC为底的等腰△ABC,使得点B落在直线l3上(保留作图痕迹,不写作法);
(2)若(1)中得到的△ABC为等腰直角三角形,求AC的长.
考点:全等三角形的判定与性质,平行线之间的距离,等腰直角三角形
专题:
分析:(1)作出线段AC的垂直平分线,使得点B落在直线l3上,连结AB,BC,△ABC即为所求;
(2)过点C作CD⊥l3于D,过点A作AE⊥l3于E,根据同角的余角相等求出∠ABE=∠BCD,然后利用“角角边”证明△ABE和△BCD全等,根据全等三角形对应边相等可得AE=BD,再利用勾股定理列式求出BC的长,然后根据等腰直角三角形的斜边等于直角边的
倍解答.
(2)过点C作CD⊥l3于D,过点A作AE⊥l3于E,根据同角的余角相等求出∠ABE=∠BCD,然后利用“角角边”证明△ABE和△BCD全等,根据全等三角形对应边相等可得AE=BD,再利用勾股定理列式求出BC的长,然后根据等腰直角三角形的斜边等于直角边的
| 2 |
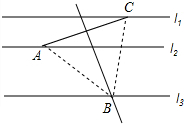
解答:解:(1)如图所示:△ABC即为所求.
(2)如图,过点C作CD⊥l3于D,过点A作AE⊥l3于E,
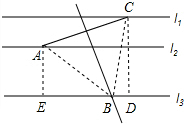
则∠BCD+∠CBD=90°,
∵△ABC为等腰直角三角形,
∴∠ABE+∠CBD=180°-90°=90°,
∴∠ABE=∠BCD,
在△ABE和△BCD中,
,
∴△ABE≌△BCD(AAS),
∴AE=BD,
∵l1,l2之间的距离为1,l2,l3之间的距离为2,
∴BD=2,CD=1+2=3,
在Rt△BCD中,BC=
=
=
,
∵△ABC是等腰直角三角形,
∴AC=
BC=
.

(2)如图,过点C作CD⊥l3于D,过点A作AE⊥l3于E,

则∠BCD+∠CBD=90°,
∵△ABC为等腰直角三角形,
∴∠ABE+∠CBD=180°-90°=90°,
∴∠ABE=∠BCD,
在△ABE和△BCD中,
|
∴△ABE≌△BCD(AAS),
∴AE=BD,
∵l1,l2之间的距离为1,l2,l3之间的距离为2,
∴BD=2,CD=1+2=3,
在Rt△BCD中,BC=
| BD2+CD2 |
| 22+32 |
| 13 |
∵△ABC是等腰直角三角形,
∴AC=
| 2 |
| 26 |
点评:本题考查了全等三角形的判定与性质,线段垂直平分线的画法,平行线间的距离,等腰三角形的性质,作辅助线构造出全等三角形是解题的关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
当x<0时,函数y=-
的图象在( )
| 5 |
| x |
| A、第四象限 | B、第三象限 |
| C、第二象限 | D、第一象限 |
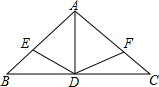 如图,在△ABC中,AB=AC,AD是角平分线,点E、F分别在AB、AC上,且BE=CF,则下列说法正确的有( )
如图,在△ABC中,AB=AC,AD是角平分线,点E、F分别在AB、AC上,且BE=CF,则下列说法正确的有( )①AD所在直线为线段BC的垂直平分线;
②△AED≌△AFD;
③∠BDE与∠BDF互补;
④S△CDF=
| 1 |
| 3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
对于任何整数m,多项式(4m+5)2-9都能( )
| A、被8整除 |
| B、被m整除 |
| C、被(m-1)整除 |
| D、被(2m-1)整除 |
 如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,且a+b=3
如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,且a+b=3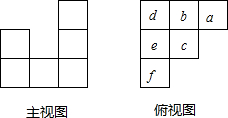 用一些相同的小立方体搭一个几何体,它的主视图和俯视图如图所示,俯视图中小正方形中字母表示在该位置的小立方块的个数,请解答下列问题:
用一些相同的小立方体搭一个几何体,它的主视图和俯视图如图所示,俯视图中小正方形中字母表示在该位置的小立方块的个数,请解答下列问题:
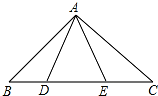 已知:如图,点D,E在△ABC的BC边上,AB=AC,AD=AE.请再写出一组相等的线段,并证明.
已知:如图,点D,E在△ABC的BC边上,AB=AC,AD=AE.请再写出一组相等的线段,并证明. 如图所示,在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别是a,b,c,已知b=2
如图所示,在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别是a,b,c,已知b=2