题目内容
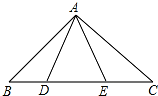 已知:如图,点D,E在△ABC的BC边上,AB=AC,AD=AE.请再写出一组相等的线段,并证明.
已知:如图,点D,E在△ABC的BC边上,AB=AC,AD=AE.请再写出一组相等的线段,并证明.考点:全等三角形的判定与性质
专题:计算题
分析:BD=CE或BE=CD,理由为:由AB=AC,AD=AE,利用等边对等角得到两对角相等,再由AB=AC,利用AAS得到三角形ABE与三角形ACD全等,利用全等三角形对应边相等即可得证.
解答:解:BD=CE或BE=CD,理由为:
证明:∵AB=AC,
∴∠B=∠C,
∵AD=AE,
∴∠ADE=∠AED,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(AAS),
∴BE=CD,
∴BE-DE=DC-DE,即BD=CE.
证明:∵AB=AC,
∴∠B=∠C,
∵AD=AE,
∴∠ADE=∠AED,
在△ABE和△ACD中,
|
∴△ABE≌△ACD(AAS),
∴BE=CD,
∴BE-DE=DC-DE,即BD=CE.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
在形状、大小、颜色都一样的卡片上,分别画有等边三角形、平行四边形、菱形、矩形、等腰梯形这五个图形,画面朝下随意放在桌面上,小芳随机抽取一张卡片.用P1、P2、P3分别表示事件(1)“抽得图形是中心对称图形”(2)“抽得图形是轴对称图形”(3)“抽得图形既是中心对称图形,又是轴对称图形”发生的可能性大小,按可能性从小到大的顺序排列是( )
| A、P3<P2<P1 |
| B、P1<P2<P3 |
| C、P2<P3<P1 |
| D、P3<P1<P2. |
 观察如图所摆放的五朵梅花,平移中间的一朵梅花,下列说法错误的是( )
观察如图所摆放的五朵梅花,平移中间的一朵梅花,下列说法错误的是( )| A、沿对角线平移到左上角即可得到左上角梅花 |
| B、沿对角线平移到右上角,再顺时针旋转90°可得到右上角梅花 |
| C、沿对角线平移到右下角,再旋转180°可得到右下角梅花 |
| D、沿对角线平移到左下角,再顺时针旋转90°可得到左下角梅花 |
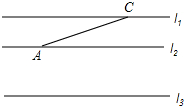 如图,已知直线l1∥l2∥l3,且l1,l2之间的距离为1,l2,l3之间的距离为2,点A、C分别在直线l2,l1上,
如图,已知直线l1∥l2∥l3,且l1,l2之间的距离为1,l2,l3之间的距离为2,点A、C分别在直线l2,l1上, 已知:如图,∠ACB=∠DBC,AC=DB. 求证:AB=DC.
已知:如图,∠ACB=∠DBC,AC=DB. 求证:AB=DC. 在四边形ABCD中,AB∥CD,AD∥BC,点E是线段BC的中点,F点在边DC上,AE平分∠BAF.
在四边形ABCD中,AB∥CD,AD∥BC,点E是线段BC的中点,F点在边DC上,AE平分∠BAF. 已知,在如图四边形ABCD中,AB∥CD,AB=CD,点A,B,C在⊙O上,AD是⊙O切线,射线AO交BC于点E,交⊙O于点F.点P在射线AO上,
已知,在如图四边形ABCD中,AB∥CD,AB=CD,点A,B,C在⊙O上,AD是⊙O切线,射线AO交BC于点E,交⊙O于点F.点P在射线AO上,