题目内容
如图，在Rt△ABC中，∠C=90°，∠A，∠B，∠C的对边分别为a，b，c，且a+b=3| 3 |
| 15 |
考点：勾股定理
专题：
分析：利用勾股定理以及三角形面积公式进而得出（
）2+2ab=27，进而得出△ABC的面积．
| 15 |
解答：解：∵在Rt△ABC中，∠C=90°，∠A，∠B，∠C的对边分别为a，b，c，
∴a2+b2=c2，
∵a+b=3
，c=
，
∴（a+b）2=（3
）2
则a2+b2+2ab=27，
∴（
）2+2ab=27，
整理得：2ab=12，
故△ABC的面积为：
ab=3．
∴a2+b2=c2，
∵a+b=3
| 3 |
| 15 |
∴（a+b）2=（3
| 3 |
则a2+b2+2ab=27，
∴（
| 15 |
整理得：2ab=12，
故△ABC的面积为：
| 1 |
| 2 |
点评：此题主要考查了勾股定理以及完全平方公式的应用，得出ab的值是解题关键．
练习册系列答案
相关题目
在同样的条件下对某种小麦种子进行发芽试验，统计发芽种子数，获得如下频数表，由表估计该麦种的发芽概率是（ ）
| 试验种子数n（粒） | 50 | 200 | 500 | 1000 | 3000 | ||
| 发芽频数m | 45 | 188 | 476 | 951 | 2850 | ||
发芽频率
| 0.9 | 0.94 | 0.952 | 0.951 | 0.95 |
| A、0.8 | B、0.9 |
| C、0.95 | D、1 |
用6个大小相同的正方体搭成如图所示的几何体，下列说法正确的是（ ）| A、主视图的面积最大 |
| B、左视图的面积最大 |
| C、俯视图的面积最大 |
| D、主视图、俯视图的面积相等 |
如图，E，F是四边形ABCD的对角线AC上两点，AF=CE，DF=BE，DF∥BE．求证：AB=CD．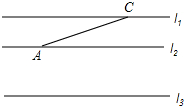
如图，已知直线l1∥l2∥l3，且l1，l2之间的距离为1，l2，l3之间的距离为2，点A、C分别在直线l2，l1上，