题目内容
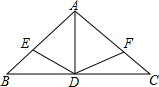 如图,在△ABC中,AB=AC,AD是角平分线,点E、F分别在AB、AC上,且BE=CF,则下列说法正确的有( )
如图,在△ABC中,AB=AC,AD是角平分线,点E、F分别在AB、AC上,且BE=CF,则下列说法正确的有( )①AD所在直线为线段BC的垂直平分线;
②△AED≌△AFD;
③∠BDE与∠BDF互补;
④S△CDF=
| 1 |
| 3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:全等三角形的判定与性质,线段垂直平分线的性质,等腰三角形的性质
专题:
分析:由在△ABC中,AB=AC,AD是角平分线,根据三线合一的性质,可得AD所在直线为线段BC的垂直平分线;又由BE=CF,易证得△AED≌△AFD(SAS),即可得∠ADE=∠ADF,即可证得∠BDE=∠CDF,则可得∠BDE与∠BDF互补;因为CF:AC的值不确定,根据等高三角形的面积比等于对应底的比,可知S△CDF不一定等于
S△ADC.
| 1 |
| 3 |
解答:解:①∵在△ABC中,AB=AC,AD是角平分线,
∴AD⊥BC,BD=CD,
即AD所在直线为线段BC的垂直平分线;故正确;
②∵AB=AC,BE=CF,
∴AE=AF,
在△AED和△AFD中,
,
∴△AED≌△AFD(SAS),故正确;
③∵△AED≌△AFD,
∴∠ADE=∠ADF,
∵∠ADB=∠ADC=90°,
∴∠BDE=∠CDF,
∴∠BDE+∠BDF=∠CDF+∠BDF=180°,
即∠BDE与∠BDF互补;故正确;
④∵CF:AC的值不确定,
∴S△CDF不一定等于
S△ADC.故错误.
故选C.
∴AD⊥BC,BD=CD,
即AD所在直线为线段BC的垂直平分线;故正确;

②∵AB=AC,BE=CF,
∴AE=AF,
在△AED和△AFD中,
|
∴△AED≌△AFD(SAS),故正确;
③∵△AED≌△AFD,
∴∠ADE=∠ADF,
∵∠ADB=∠ADC=90°,
∴∠BDE=∠CDF,
∴∠BDE+∠BDF=∠CDF+∠BDF=180°,
即∠BDE与∠BDF互补;故正确;
④∵CF:AC的值不确定,
∴S△CDF不一定等于
| 1 |
| 3 |
故选C.
点评:此题考查了全等三角形的判定与性质以及等腰三角形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
点(3,4)关于x轴对称的点的坐标为( )
| A、(-3,4) |
| B、(-3,-4) |
| C、(3,-4) |
| D、(4,3) |
 用6个大小相同的正方体搭成如图所示的几何体,下列说法正确的是( )
用6个大小相同的正方体搭成如图所示的几何体,下列说法正确的是( )| A、主视图的面积最大 |
| B、左视图的面积最大 |
| C、俯视图的面积最大 |
| D、主视图、俯视图的面积相等 |
 观察如图所摆放的五朵梅花,平移中间的一朵梅花,下列说法错误的是( )
观察如图所摆放的五朵梅花,平移中间的一朵梅花,下列说法错误的是( )| A、沿对角线平移到左上角即可得到左上角梅花 |
| B、沿对角线平移到右上角,再顺时针旋转90°可得到右上角梅花 |
| C、沿对角线平移到右下角,再旋转180°可得到右下角梅花 |
| D、沿对角线平移到左下角,再顺时针旋转90°可得到左下角梅花 |
 如图,E,F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.求证:AB=CD.
如图,E,F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.求证:AB=CD. 如图,已知直线l1∥l2∥l3,且l1,l2之间的距离为1,l2,l3之间的距离为2,点A、C分别在直线l2,l1上,
如图,已知直线l1∥l2∥l3,且l1,l2之间的距离为1,l2,l3之间的距离为2,点A、C分别在直线l2,l1上, 已知:如图,∠ACB=∠DBC,AC=DB. 求证:AB=DC.
已知:如图,∠ACB=∠DBC,AC=DB. 求证:AB=DC.