题目内容
3. 如图,PA,PB分别与⊙O相切于点A,B,AC是⊙O的直径,若tan∠ACB=$\sqrt{5}$,求tan∠PCB的值.
如图,PA,PB分别与⊙O相切于点A,B,AC是⊙O的直径,若tan∠ACB=$\sqrt{5}$,求tan∠PCB的值.
分析 由切线的性质及圆周角定理可证明∠AOP=∠ACB,即可得OP∥CB、∠PCB=∠CPO、∠ACB=∠AOP,设OA=OC=r,由tan∠ACB=$\sqrt{5}$得AP=$\sqrt{5}$r、PC=3r,作OD⊥PC,证△OCD∽△PCA得$\frac{OC}{PC}=\frac{OD}{AP}=\frac{CD}{CA}$,即可知OD=$\frac{\sqrt{5}}{3}$r、CD=$\frac{2}{3}$r、PD=$\frac{7}{3}$r,由正切定义可得答案.
解答 解:如图,连接OB、OP、AB,
∵PA、PB是⊙O的切线,
∴∠PAO=90°,∠AOP=∠BOP=$\frac{1}{2}$∠AOB,
又∵∠ACB=$\frac{1}{2}$∠AOB,
∴∠AOP=∠ACB,
∴OP∥CB,
∴∠PCB=∠CPO,∠ACB=∠AOP,
设OA=OC=r,
∵tan∠ACB=tan∠AOP=$\frac{AP}{AO}$=$\sqrt{5}$,
∴AP=$\sqrt{5}$r,PC=$\sqrt{A{P}^{2}+A{C}^{2}}$=$\sqrt{(\sqrt{5}r)^{2}+(2r)^{2}}$=3r,
作OD⊥PC于点D,
∵∠CDO=∠CAP=90°,∠OCD=∠PCA,
∴△OCD∽△PCA,
∴$\frac{OC}{PC}=\frac{OD}{AP}=\frac{CD}{CA}$,即$\frac{r}{3r}=\frac{OD}{\sqrt{5}r}=\frac{CD}{2r}$,
∴OD=$\frac{\sqrt{5}}{3}$r,CD=$\frac{2}{3}$r,
∴PD=PC-CD=3r-$\frac{2}{3}$r=$\frac{7}{3}$r,
则tan∠PCB=tan∠CPD=$\frac{OD}{PD}$=$\frac{\frac{\sqrt{5}}{3}r}{\frac{7}{3}r}$=$\frac{\sqrt{5}}{7}$.
点评 本题主要考查切线的性质,熟练掌握切线长定理、平行线的判定与性质、圆周角定理及相似三角形的性质和判定、勾股定理、三角函数的应用是解题的关键.

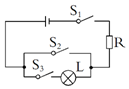 在物理课上,某实验的电路图如图所示,其中S1,S2,S3表示电路的开关,L表示小灯泡,R为保护电阻.若闭合开关S1,S2,S3中的任意两个,则小灯泡L发光的概率( )
在物理课上,某实验的电路图如图所示,其中S1,S2,S3表示电路的开关,L表示小灯泡,R为保护电阻.若闭合开关S1,S2,S3中的任意两个,则小灯泡L发光的概率( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
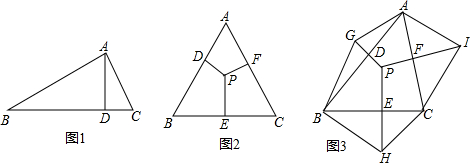
 (1)在等腰梯形ABCD中,若AD∥BC,PA=PD.求证:PB=PC
(1)在等腰梯形ABCD中,若AD∥BC,PA=PD.求证:PB=PC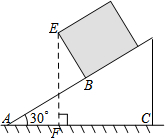 一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3m,己知木箱高BE=$\sqrt{3}$m,斜面坡角为30°,则木箱端点E距地面AC的高度为3m.
一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3m,己知木箱高BE=$\sqrt{3}$m,斜面坡角为30°,则木箱端点E距地面AC的高度为3m. 如图,AC、BC分别平分∠MAB和∠ABN,∠ACB=90°.
如图,AC、BC分别平分∠MAB和∠ABN,∠ACB=90°.