Question

19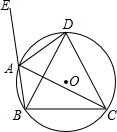．如图，AD是圆内接△ABC的∠BAC的外角平分线，交圆于点D．求证：△BDC是等腰三角形．

Answer 1

分析 根据圆内接四边形的性质得到∠EAD=∠BCD，由圆周角定理得到∠DAC=∠DBC，根据角平分线的定义得到∠EAD=∠DAC，根据等腰三角形的判定定理证明．

解答 证明：∵四边形ABCD是圆内接四边形，
∴∠EAD=∠BCD，
由圆周角定理得，∠DAC=∠DBC，
∵AD是圆内接△ABC的∠BAC的外角平分线，
∴∠EAD=∠DAC，
∴∠DBC=∠BCD，
∴DB=DC，即△BDC是等腰三角形．

点评 本题看的是三角形的外接圆与外心的概念和性质，掌握圆内接四边形的性质、圆周角定理是解题的关键．