题目内容
20. 如图,已知∠MON=60°,P是∠MON内一点,P到OM的距离PA=2,P到ON的距离PB=11,求OP的长.
如图,已知∠MON=60°,P是∠MON内一点,P到OM的距离PA=2,P到ON的距离PB=11,求OP的长.
分析 延长BP交OM于C,解直角三角形求出BC,OA的长,再求OP的长即可.
解答 解:
延长BP交OM于C,
∵∠MON=6O°,PB⊥ON,
∴∠OCB=30°,
∵PA⊥OM,PA=2,
∴PC=4,AC=2$\sqrt{3}$,
∵PB=11,
∴BC=PB+PC=11+4=15,
∵∠OCB=30°,PB⊥ON,
∴OC=10$\sqrt{3}$,
∵AC=2$\sqrt{3}$,
∴OA=OC-AC=8$\sqrt{3}$,
∵PA=2,PA⊥OM,
∴OP=$\sqrt{O{A}^{2}+A{P}^{2}}$=$\sqrt{192+4}$=14,
∴P点到∠MON的顶点OP的长度为14.
点评 本题考查了勾股定理的运用以及解直角三角形综合应用问题.难度很大,有利于培养同学们钻研和探索问题的精神.

练习册系列答案
相关题目
4.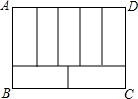 如图,周长为34cm的长方形ABCD被分成7个形状大小完全相同的小长方形,则长方形ABCD的面积为( )
如图,周长为34cm的长方形ABCD被分成7个形状大小完全相同的小长方形,则长方形ABCD的面积为( )
 如图,周长为34cm的长方形ABCD被分成7个形状大小完全相同的小长方形,则长方形ABCD的面积为( )
如图,周长为34cm的长方形ABCD被分成7个形状大小完全相同的小长方形,则长方形ABCD的面积为( )| A. | 49cm2 | B. | 74cm2 | C. | 68cm2 | D. | 70cm2 |
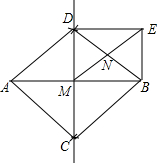 如图,分别以线段AB两端点A、B 为圆心,以大于长为半径画弧交于C、D两点,作直线CD交AB于M,DE∥AB,BE∥CD,
如图,分别以线段AB两端点A、B 为圆心,以大于长为半径画弧交于C、D两点,作直线CD交AB于M,DE∥AB,BE∥CD,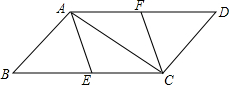 如图,?ABCD中已知E、F分别是BC、AD的中点,且AB⊥AC.求证:四边形AECF是菱形.
如图,?ABCD中已知E、F分别是BC、AD的中点,且AB⊥AC.求证:四边形AECF是菱形.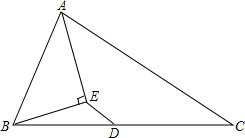 如图,△ABC中,D是BC边的中点,AE平分∠BAC,BE⊥AE于E,若AB=5,AC=7,求ED.
如图,△ABC中,D是BC边的中点,AE平分∠BAC,BE⊥AE于E,若AB=5,AC=7,求ED.