题目内容
11．在△ABC中，AB=6cm，∠B=83°，若将△ABC向右平移5cm得到△A′B′C′，则A′B′=6cm，AA′=5cm，∠B′=83°．分析 根据平移的性质，对应点的连线互相平行且相等，平移变换只改变图形的位置不改变图形的形状与大小对各小题分析判断即可得解．
解答 解：∵将△ABC向右平移5cm得到△A′B′C′，
∴△ABC≌△A′B′C′，AA′=5cm，
∴A′B′=AB=6cm，∠B′=∠B=83°，
故答案为：6，5，83．
点评 本题考查了平移的性质，根据对应点找出平移变化的相等的线段是解题的关键．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
1．如果等式（2a-1）a+2=1成立，则a的值可能有（ ）
| A． | 4个 | B． | 1个 | C． | 2个 | D． | 3个 |
19．体育课上，全班男同学进行了100米测试，达标成绩为15秒．下表是某小组所有男生的成绩，其中“+”表示成绩大于15秒．这个小组男生的达标率为37.5%．（$达标率=\frac{达标人数}{总人数}×100%$）
| -0.8 | +1 | -1.2 | 0 | -0.7 | +0.6 | -0.4 | -0.1 |
16．《九章算术》中的算筹图是竖排的，为看图方便，我们把它改为横排，如图1，图2所示，图中各行从左到右列出的算筹数分别表示未知数x，y的系数与相应的常数项．把图1表示的算筹图用我们现在所熟悉的方程组形式表述出来，就是$\left\{\begin{array}{l}{3x+2y=19}\\{x+4y=23}\end{array}\right.$．类似地，图2所示的算筹图我们可以表述为（ ）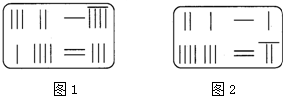
| A． | $\left\{\begin{array}{l}{2x+y=11}\\{4x+3y=27}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{2x+y=11}\\{4x+3y=22}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{3x+2y=19}\\{x+4y=23}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{2x+y=6}\\{4x+3y=27}\end{array}\right.$ |
3．
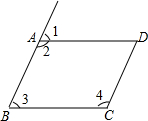如图，在四边形ABCD中，AB∥CD，AD∥BC，下列各式不一定正确的是（ ）
如图，在四边形ABCD中，AB∥CD，AD∥BC，下列各式不一定正确的是（ ）| A． | ∠1+∠2=180° | B． | ∠2+∠3=180° | C． | ∠3+∠4=180° | D． | ∠2+∠4=180° |
如图，已知∠MON=60°，P是∠MON内一点，P到OM的距离PA=2，P到ON的距离PB=11，求OP的长．