题目内容
8.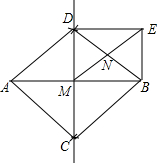 如图,分别以线段AB两端点A、B 为圆心,以大于长为半径画弧交于C、D两点,作直线CD交AB于M,DE∥AB,BE∥CD,
如图,分别以线段AB两端点A、B 为圆心,以大于长为半径画弧交于C、D两点,作直线CD交AB于M,DE∥AB,BE∥CD,(1)判断四边形ACBD的形状并说明理由;
(2)求证:ME=AD.
分析 (1)根据题意得出AC=BC=BD=AD,即可得出结论;
(2)先证明四边形BEDM是平行四边形,再由菱形的性质得出∠BMD=90°,证明四边形ACBD是矩形,得出对角线相等ME=BD,即可得出结论.
解答 (1)解:四边形ACBD是菱形;理由如下:
根据题意得:AC=BC=BD=AD,
∴四边形ACBD是菱形(四条边相等的四边形是菱形);
(2)证明:∵DE∥AB,BE∥CD,
∴四边形BEDM是平行四边形,
∵四边形ACBD是菱形,
∴AB⊥CD,
∴∠BMD=90°,
∴四边形ACBD是矩形,
∴ME=BD,
∵AD=BD,
∴ME=AD.
点评 本题考查了菱形的判定、矩形的判定与性质、平行四边形的判定;熟练掌握菱形的判定和矩形的判定与性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
19.体育课上,全班男同学进行了100米测试,达标成绩为15秒.下表是某小组所有男生的成绩,其中“+”表示成绩大于15秒.这个小组男生的达标率为37.5%.($达标率=\frac{达标人数}{总人数}×100%$)
| -0.8 | +1 | -1.2 | 0 | -0.7 | +0.6 | -0.4 | -0.1 |
16.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1,图2所示,图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1表示的算筹图用我们现在所熟悉的方程组形式表述出来,就是$\left\{\begin{array}{l}{3x+2y=19}\\{x+4y=23}\end{array}\right.$.类似地,图2所示的算筹图我们可以表述为( )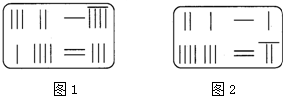

| A. | $\left\{\begin{array}{l}{2x+y=11}\\{4x+3y=27}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+y=11}\\{4x+3y=22}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{3x+2y=19}\\{x+4y=23}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x+y=6}\\{4x+3y=27}\end{array}\right.$ |
3.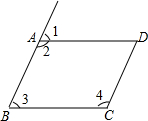 如图,在四边形ABCD中,AB∥CD,AD∥BC,下列各式不一定正确的是( )
如图,在四边形ABCD中,AB∥CD,AD∥BC,下列各式不一定正确的是( )
 如图,在四边形ABCD中,AB∥CD,AD∥BC,下列各式不一定正确的是( )
如图,在四边形ABCD中,AB∥CD,AD∥BC,下列各式不一定正确的是( )| A. | ∠1+∠2=180° | B. | ∠2+∠3=180° | C. | ∠3+∠4=180° | D. | ∠2+∠4=180° |
 如图,已知等腰梯形ABCD中,AD∥BC,AB=DC,点E为BC的中点,求证:AE=DE.
如图,已知等腰梯形ABCD中,AD∥BC,AB=DC,点E为BC的中点,求证:AE=DE. 如图,已知∠MON=60°,P是∠MON内一点,P到OM的距离PA=2,P到ON的距离PB=11,求OP的长.
如图,已知∠MON=60°,P是∠MON内一点,P到OM的距离PA=2,P到ON的距离PB=11,求OP的长.