题目内容
15．
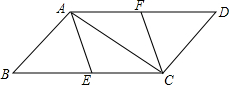如图，?ABCD中已知E、F分别是BC、AD的中点，且AB⊥AC．求证：四边形AECF是菱形．
分析 先利用平行四边形的性质得AD∥BC，AD=BC，再由E、F分别是BC、AD的中点易得AF∥CE，AF=CE，则可判断四边形AECF为平行四边形，再利用直角三角形斜边上的中线性质得AE=EC，于是可根据菱形的判定方法得到结论．
解答 证明：∵四边形ABCD为平行四边形，
∴AD∥BC，AD=BC，
∵E、F分别是BC、AD的中点，
∴AF∥CE，AF=CE，
∴四边形AECF为平行四边形，
∵AB⊥AC，
∴∠BAC=90°，
而E为BC的中点，
∴BE=AE=EC，
∴四边形AECF是菱形．
点评 本题考查了菱形的判断：一组邻边相等的平行四边形是菱形；四条边都相等的四边形是菱形；对角线互相垂直的平行四边形是菱形．也考查了平行四边形的性质．
练习册系列答案
智慧小复习系列答案
相关题目
3．
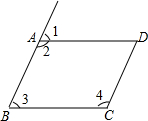如图，在四边形ABCD中，AB∥CD，AD∥BC，下列各式不一定正确的是（ ）
如图，在四边形ABCD中，AB∥CD，AD∥BC，下列各式不一定正确的是（ ）| A． | ∠1+∠2=180° | B． | ∠2+∠3=180° | C． | ∠3+∠4=180° | D． | ∠2+∠4=180° |
如图，已知∠MON=60°，P是∠MON内一点，P到OM的距离PA=2，P到ON的距离PB=11，求OP的长．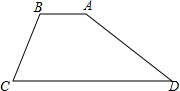
水坝的横截面为梯形ABCD，迎水坡AD的坡角为30°，背水坡BC的坡度为1：1，坝顶宽AB为4m，坝高为6m