题目内容
15.若关于x、y的二元一次方程组$\left\{\begin{array}{l}{ax+y=3a-1}\\{2x-y=2}\end{array}\right.$的解满足x+y=1,则a的值为$\frac{1}{2}$.分析 首先由$\left\{\begin{array}{l}{2x-y=2}\\{x+y=1}\end{array}\right.$求出二元一次方程的解是多少;然后把求出的x、y的值代入ax+y=3a-1,求出a的值为多少即可.
解答 解:∵关于x、y的二元一次方程组$\left\{\begin{array}{l}{ax+y=3a-1}\\{2x-y=2}\end{array}\right.$的解满足x+y=1,
∴$\left\{\begin{array}{l}{2x-y=2}\\{x+y=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=1}\\{y=0}\end{array}\right.$
∴a×1+0=3a-1
解得a=$\frac{1}{2}$,
∴a的值为$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 此题主要考查了二元一次方程组的解,要熟练掌握,当遇到有关二元一次方程组的解的问题时,要回到定义中去,通常采用代入法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下列事件为必然事件的是( )
| A. | 任意买一张电影票,座位号是偶数 | |
| B. | 打开电视机,正在播放动画片 | |
| C. | 两边及其夹角对应相等的两个三角形全等 | |
| D. | 三根长度为2cm、2cm、4cm的木棒能摆成三角形 |
 如图,在直角△ABC中,∠BAC=90°,CB=10,AC=6,DE是AB边的垂直平分线,垂足为D,交BC于点E,连接AE,则△ACE的周长为16.
如图,在直角△ABC中,∠BAC=90°,CB=10,AC=6,DE是AB边的垂直平分线,垂足为D,交BC于点E,连接AE,则△ACE的周长为16. 如图,等腰直角三角形的斜边长AB=8,一直线l绕顶点B任意旋转,过A向l作垂线,垂足为H,则线段CH长的取值范围是0≤CH≤8.
如图,等腰直角三角形的斜边长AB=8,一直线l绕顶点B任意旋转,过A向l作垂线,垂足为H,则线段CH长的取值范围是0≤CH≤8. 如图,四边形ABCD是平行四边形.
如图,四边形ABCD是平行四边形. 尺规作图:已知△ABC,如图.
尺规作图:已知△ABC,如图.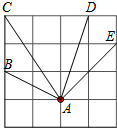 如图,在4×4的网格图中,小正方形的边长为1,则图中用字母表示的四条线段中长度为$\sqrt{10}$的线段是AD.
如图,在4×4的网格图中,小正方形的边长为1,则图中用字母表示的四条线段中长度为$\sqrt{10}$的线段是AD.