题目内容
1.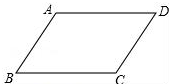 如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.(1)写出所有成立的情况(只需填写序号)
(2)选择其中一种证明.
已知:在四边形ABCD中,AD∥BC,∠A=∠C;
求证:四边形ABCD是平行四边形.
分析 (1)由平行四边形的判定方法容易得出结果;
(2)可以选择:①,③作为条件,首先根据∠B+∠C=180°可得AB∥DC,再根据AD∥BC,可根据两组对边分别平行的四边形是平行四边形判定出四边形ABCD是平行四边形.此题答案不唯一.
解答 (1)解:①③;③④;①④;②④;
(2)选择:①,③,
证明:∵∠B+∠C=180°,
∴AB∥DC,
又∵AD∥BC,
∴四边形ABCD是平行四边形;
故答案为:AD∥BC,∠A=∠C.
点评 此题主要考查了平行四边形的判定,关键是掌握两组对边分别平行的四边形是平行四边形.两组对边分别相等的四边形是平行四边形.一组对边平行且相等的四边形是平行四边形.两组对角分别相等的四边形是平行四边形.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
16. 如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )
如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )
 如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )
如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )| A. | 中位数是6.5 | |
| B. | 平均数高于众数 | |
| C. | 极差为3 | |
| D. | 平均每周锻炼超过6小时的人占总数的一半 |
11. 如图,直线a∥b,∠1=80°,∠2=40°,则∠3等于( )
如图,直线a∥b,∠1=80°,∠2=40°,则∠3等于( )
 如图,直线a∥b,∠1=80°,∠2=40°,则∠3等于( )
如图,直线a∥b,∠1=80°,∠2=40°,则∠3等于( )| A. | 130° | B. | 120° | C. | 110° | D. | 100° |
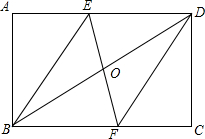 如图所示,将矩形ABCD沿EF对折,使点B与点D重合,折痕为EF,请判断四边形BFDE的形状,并证明你的结论.
如图所示,将矩形ABCD沿EF对折,使点B与点D重合,折痕为EF,请判断四边形BFDE的形状,并证明你的结论.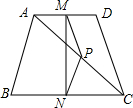 如图,在四边形ABCD中,AB=DC,P是对角线AC的中点,M是AD的中点,N是BC的中点.
如图,在四边形ABCD中,AB=DC,P是对角线AC的中点,M是AD的中点,N是BC的中点.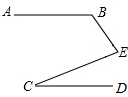 如图所示,AB∥CD,若∠B=120°,∠C=35°,则∠E=95°.
如图所示,AB∥CD,若∠B=120°,∠C=35°,则∠E=95°. AB∥CD,∠1=58°,FG平分∠EFD,则∠FGB的度数为151°.
AB∥CD,∠1=58°,FG平分∠EFD,则∠FGB的度数为151°.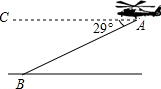 一架直升机到某失事地点进行搜救,直升机飞到A处时,探测前方地面上B处有一生命体,从A处观测B处的俯角为29°,该直升机一直保持在距地面100米高度直线飞行搜索,飞行速度为10米/秒,求该直升机从A处飞到生命体的正上方时所用的时间.(结果精确到0.1秒)
一架直升机到某失事地点进行搜救,直升机飞到A处时,探测前方地面上B处有一生命体,从A处观测B处的俯角为29°,该直升机一直保持在距地面100米高度直线飞行搜索,飞行速度为10米/秒,求该直升机从A处飞到生命体的正上方时所用的时间.(结果精确到0.1秒)