题目内容
12．
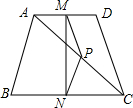如图，在四边形ABCD中，AB=DC，P是对角线AC的中点，M是AD的中点，N是BC的中点．（1）若AB=6，求PM的长；
（2）若∠PMN=20°，求∠MPN的度数．
分析 （1）由题意可知PM是△ADC的中位线，进而可求出MP的长；
（2）易证△PMN是等腰三角形，由等腰三角形的性质即可求出∠MPN的度数．
解答 解：（1）∵AB=DC，AB=6，
∴DC=6，
∵点P是AC的中点，点M是AD的中点，
∴PM=$\frac{1}{2}$DC=$\frac{1}{2}$×6=3；
（2）∵点P是AC的中点，点N是BC的中点，
∴PN=$\frac{1}{2}$BC，
∵AB=DC，
∴PM=PN，
∴∠PNM=∠PMN=20°，
∴∠MPN=180°-∠PMN-∠PNM=140°．
点评 此题主要考查了三角形中位线定理，以及等腰三角形的判定与性质，熟练掌握性质定理是解题的关键．
练习册系列答案
高中必刷题系列答案
相关题目
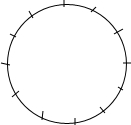八年级（3）班48人参加课外活动，有16人打篮球，8人打乒乓球，4人跳绳，12人打排球，其余人参加长跑，请在如图的十二等分的圆周上，用扇形统计图表示学生参加课外活动的情况．
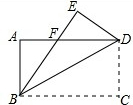如图，将矩形纸片ABCD沿对角线BD折叠，点C落在点E处，BE交AD于点F．求证：AF=EF．
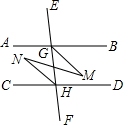如图，已知∠EGB+∠CHE=180°，GM平分∠BGF，HN平分∠CHE．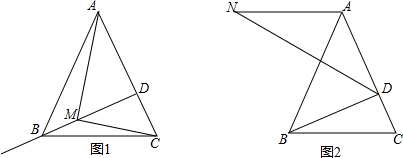
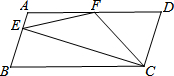如图，在?ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论：
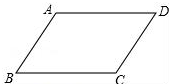如图，请在下列四个关系中，选出两个恰当的关系作为条件，推出四边形ABCD是平行四边形，并予以证明．关系：①AD∥BC，②AB=CD，③∠A=∠C，④∠B+∠C=180°．