题目内容
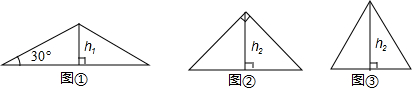
16.请你仔细观察下面图形:如图①所示,是一个底角为30°,腰长为1的等腰三角形,它的底边上的高为h1;
如图②所示,是一个腰长为1的等腰直角三角形,它的底边上的高为h2;
如图③所示,是一个腰长为1的等边三角形,它的高为h3
(1)h1=$\frac{1}{2}$;h2=$\frac{\sqrt{2}}{2}$;h3=$\frac{\sqrt{3}}{2}$
(2)问:h1,h2,h3能不能构成一个直角三角形的三条边?请你说明理由.
分析 (1)由特殊锐角的三角函数容易得出结果;
(2)由勾股定理的逆定理容易得出结论.
解答 解:(1)根据题意和三角函数得:sin30°=$\frac{{h}_{1}}{1}$,sin45°=$\frac{{h}_{2}}{1}$,sin60°=$\frac{{h}_{3}}{1}$,
∴h1=$\frac{1}{2}$,h2=$\frac{\sqrt{2}}{2}$,h3=$\frac{\sqrt{3}}{2}$;
故答案为:$\frac{1}{2}$,$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$;
(2)h1,h2,h3能构成一个直角三角形的三条边;理由如下:
∵h12+h22=($\frac{1}{3}$)2+($\frac{\sqrt{2}}{2}$)2=$\frac{3}{4}$=($\frac{\sqrt{3}}{2}$)2=h32,
∴h1,h2,h3能构成一个直角三角形的三条边.
点评 本题考查了特殊锐角的三角函数、勾股定理的逆定理;熟记特殊锐角的三角函数值和勾股定理的逆定理是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.下列结论中,不正确的是( )
| A. | 两点确定一条直线 | |
| B. | 等角的余角相等 | |
| C. | 过一点有且只有一条直线与已知直线平行 | |
| D. | 对顶角相等 |
11.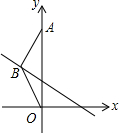 如图,在△ABO中,BA=BO,OA=3,OA在y轴的正半轴上,若点B在直线y=-$\frac{1}{2}$x+1上,△ABO的面积是( )
如图,在△ABO中,BA=BO,OA=3,OA在y轴的正半轴上,若点B在直线y=-$\frac{1}{2}$x+1上,△ABO的面积是( )
 如图,在△ABO中,BA=BO,OA=3,OA在y轴的正半轴上,若点B在直线y=-$\frac{1}{2}$x+1上,△ABO的面积是( )
如图,在△ABO中,BA=BO,OA=3,OA在y轴的正半轴上,若点B在直线y=-$\frac{1}{2}$x+1上,△ABO的面积是( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
5.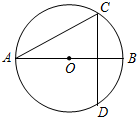 如图,AB是⊙O的直径,弦CD垂直平分OB,则∠ACD等于( )
如图,AB是⊙O的直径,弦CD垂直平分OB,则∠ACD等于( )
 如图,AB是⊙O的直径,弦CD垂直平分OB,则∠ACD等于( )
如图,AB是⊙O的直径,弦CD垂直平分OB,则∠ACD等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 70° |
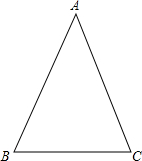 已知等腰△ABC,AB=AC=5,BC=4,请建立适当的平面直角坐标系,并求出A、B、C三点坐标.
已知等腰△ABC,AB=AC=5,BC=4,请建立适当的平面直角坐标系,并求出A、B、C三点坐标.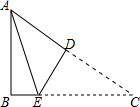 如图所示,在△ABC中,∠B=90°,AB=3,AC=5,线段AC的垂直平分线DE交AC于D交BC于E,则△ABE的周长为7.
如图所示,在△ABC中,∠B=90°,AB=3,AC=5,线段AC的垂直平分线DE交AC于D交BC于E,则△ABE的周长为7.