题目内容
5.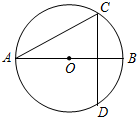 如图,AB是⊙O的直径,弦CD垂直平分OB,则∠ACD等于( )
如图,AB是⊙O的直径,弦CD垂直平分OB,则∠ACD等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 70° |
分析 连接OC,在直角△OCE中,即可求得∠COE的度数,根据等腰三角形的性质,即可求解.
解答  解:连接OC,
解:连接OC,
∵OE=$\frac{1}{2}$OB=$\frac{1}{2}$OC,
∴∠OCD=30°,
∴∠COB=60°,
∵OA=OC,
∴∠BAC=30°,
∴∠ACD=60°.
故选C.
点评 本题考查了等腰三角形的性质,正确解直角三角形,求得∠COE的度数是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.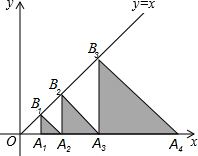 如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上.已知OA1=1,则点B2016的横坐标为( )
如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上.已知OA1=1,则点B2016的横坐标为( )
 如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上.已知OA1=1,则点B2016的横坐标为( )
如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上.已知OA1=1,则点B2016的横坐标为( )| A. | 2016 | B. | 2015$\sqrt{2}$ | C. | 22016 | D. | 22015 |
17.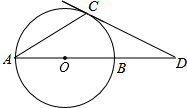 如图,AB是⊙O的直径,点C是⊙O上一点,过点C的切线与AB的延长线交于点D,连接AC、CO,若∠A=35°,则∠ADC的度数为( )
如图,AB是⊙O的直径,点C是⊙O上一点,过点C的切线与AB的延长线交于点D,连接AC、CO,若∠A=35°,则∠ADC的度数为( )
 如图,AB是⊙O的直径,点C是⊙O上一点,过点C的切线与AB的延长线交于点D,连接AC、CO,若∠A=35°,则∠ADC的度数为( )
如图,AB是⊙O的直径,点C是⊙O上一点,过点C的切线与AB的延长线交于点D,连接AC、CO,若∠A=35°,则∠ADC的度数为( )| A. | 20° | B. | 30° | C. | 35° | D. | 55° |
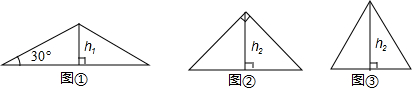
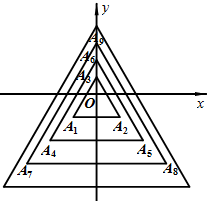 如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4、…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则顶点A22的坐标是(-8,-8).
如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4、…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则顶点A22的坐标是(-8,-8).