题目内容
1.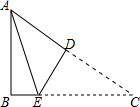 如图所示,在△ABC中,∠B=90°,AB=3,AC=5,线段AC的垂直平分线DE交AC于D交BC于E,则△ABE的周长为7.
如图所示,在△ABC中,∠B=90°,AB=3,AC=5,线段AC的垂直平分线DE交AC于D交BC于E,则△ABE的周长为7.
分析 根据勾股定理求出BC,根据线段垂直平分线得出AE=CE,求出△ABE的周长=AB+BC,代入求出即可.
解答 解:在△ABC中,∠B=90°,AB=3,AC=5,由勾股定理得:BC=4,
∵线段AC的垂直平分线DE,
∴AE=EC,
∴△ABE的周长为AB+BE+AE=AB+BE+CE=AB+BC=3+4=7,
故答案为:7.
点评 本题主要考查了线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是本题的关键.

练习册系列答案
相关题目
13.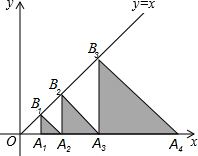 如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上.已知OA1=1,则点B2016的横坐标为( )
如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上.已知OA1=1,则点B2016的横坐标为( )
 如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上.已知OA1=1,则点B2016的横坐标为( )
如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上.已知OA1=1,则点B2016的横坐标为( )| A. | 2016 | B. | 2015$\sqrt{2}$ | C. | 22016 | D. | 22015 |
11.已知一次函数y=kx+b,当x=1时,y=-2,且它的图象与y轴交点纵坐标是-5,则它的解析式是( )
| A. | y=3x+5 | B. | y=-3x-5 | C. | y=-3x+5 | D. | y=3x-5 |
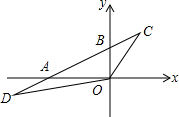 如图,在平面直角坐标系中,点O为坐标原点,直线y=kx+b经过点A(-6,0)B(0,3)两点,点C、D在直线AB上,C的纵坐标为4,点D在第三象限,且△OBC与△OAD的面积相等,则点D的坐标为(-8,-1).
如图,在平面直角坐标系中,点O为坐标原点,直线y=kx+b经过点A(-6,0)B(0,3)两点,点C、D在直线AB上,C的纵坐标为4,点D在第三象限,且△OBC与△OAD的面积相等,则点D的坐标为(-8,-1).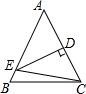 如图,等腰△ABC中,AB=AC=4cm,BC=3cm,DE是腰AC的垂直平分线,DE分别与AC、AB交于点D、E,则△BEC的周长为7cm.
如图,等腰△ABC中,AB=AC=4cm,BC=3cm,DE是腰AC的垂直平分线,DE分别与AC、AB交于点D、E,则△BEC的周长为7cm.
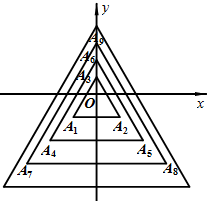 如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4、…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则顶点A22的坐标是(-8,-8).
如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4、…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则顶点A22的坐标是(-8,-8).