题目内容
4.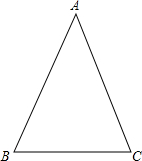 已知等腰△ABC,AB=AC=5,BC=4,请建立适当的平面直角坐标系,并求出A、B、C三点坐标.
已知等腰△ABC,AB=AC=5,BC=4,请建立适当的平面直角坐标系,并求出A、B、C三点坐标.
分析 根据题意可以建立适当的平面直角坐标系,令点B为原点,BC所在的边在x的正半轴上,然后即可写出A、B、C三点坐标.
解答  解:由题意可得,建立的平面直角坐标系如右图所示,
解:由题意可得,建立的平面直角坐标系如右图所示,
由题意可知,BC=4,AB=AC=5,作AD⊥BC于点D,
则BD=2,AD=$\sqrt{{5}^{2}-{2}^{2}}=\sqrt{25-4}=\sqrt{21}$,
∴点A的坐标是(2,$\sqrt{21}$),点B的坐标是(0,0),点C的坐标是(4,0).
点评 本题考查坐标与图形的性质,解题的关键是明确题意,建立适当的平面直角坐标系,利用数形结合的思想解答问题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
13.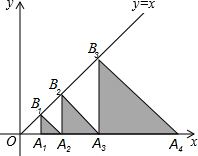 如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上.已知OA1=1,则点B2016的横坐标为( )
如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上.已知OA1=1,则点B2016的横坐标为( )
 如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上.已知OA1=1,则点B2016的横坐标为( )
如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上.已知OA1=1,则点B2016的横坐标为( )| A. | 2016 | B. | 2015$\sqrt{2}$ | C. | 22016 | D. | 22015 |
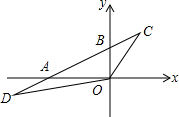 如图,在平面直角坐标系中,点O为坐标原点,直线y=kx+b经过点A(-6,0)B(0,3)两点,点C、D在直线AB上,C的纵坐标为4,点D在第三象限,且△OBC与△OAD的面积相等,则点D的坐标为(-8,-1).
如图,在平面直角坐标系中,点O为坐标原点,直线y=kx+b经过点A(-6,0)B(0,3)两点,点C、D在直线AB上,C的纵坐标为4,点D在第三象限,且△OBC与△OAD的面积相等,则点D的坐标为(-8,-1).
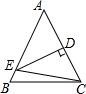 如图,等腰△ABC中,AB=AC=4cm,BC=3cm,DE是腰AC的垂直平分线,DE分别与AC、AB交于点D、E,则△BEC的周长为7cm.
如图,等腰△ABC中,AB=AC=4cm,BC=3cm,DE是腰AC的垂直平分线,DE分别与AC、AB交于点D、E,则△BEC的周长为7cm.